How to Calculate Cosine Similarity in Python
- Understanding Cosine Similarity
- Mathematics Behind Cosine Similarity
- The Need for Cosine Similarity
-
Use the
scipyLibrary to Calculate the Cosine Similarity in Python -
Use the
numpyLibrary to Calculate the Cosine Similarity in Python -
Use the
sklearnLibrary to Calculate the Cosine Similarity in Python -
Use the
torchModule to Calculate the Cosine Similarity in Python - Conclusion
Measuring the similarity between objects or documents plays a fundamental role in data science. An effective similarity measure is essential to compare text documents, analyze user preferences, or cluster similar data points.
One such measure that has gained significant popularity is cosine similarity. In this tutorial, we will explore the concept of cosine similarity, and its mathematical foundation, discover various scenarios where it proves invaluable, and explore different methods that can be used to calculate cosine similarity in Python.
Understanding Cosine Similarity
Cosine similarity is a metric determining the similarity between two non-zero vectors in a multi-dimensional space. Unlike other similarity measures, such as Euclidean distance, cosine similarity calculates the angle between two vectors rather than their magnitude.
By measuring the cosine of the angle, we obtain a value between -1 and 1, representing the degree of similarity. A value close to 1 indicates strong similarity, while a value close to -1 suggests dissimilarity.
Mathematics Behind Cosine Similarity
The mathematical principle behind cosine similarity is rooted in linear algebra and trigonometry. Given two vectors A and B, the cosine similarity (cosθ) can be calculated using the dot product and vector magnitudes as follows:
Here, (A · B) represents the dot product of vectors A and B, and ||A|| and ||B|| denote the magnitudes of the respective vectors. The resulting value represents the cosine of the angle between the two vectors, hence the term “cosine similarity.”
The Need for Cosine Similarity
Cosine similarity finds utility across various domains and applications. One notable scenario is the document similarity analysis. This technique is widely used in text mining, plagiarism detection, and recommendation systems.
For example, consider an e-commerce platform that suggests similar products to customers based on browsing history. The platform can recommend the most relevant items by calculating the cosine similarity between the vector representation of the customer’s current product of interest and other products in the catalog.
This ensures customers receive personalized recommendations based on their preferences, improving user satisfaction and increasing sales.
Use the scipy Library to Calculate the Cosine Similarity in Python
The scipy library in Python provides powerful tools for scientific computing, including functions for calculating the cosine similarity between vectors. To compute the cosine similarity using SciPy, we can utilize the scipy.spatial.distance.cosine() function.
The spatial.cosine.distance() function from the scipy module calculates the distance instead of the cosine similarity, but to achieve that, we can subtract the value of the distance from 1.
Syntax:
from scipy.spatial.distance import cosine
cosine_similarity = 1 - cosine(vector1, vector2)
In this syntax, vector1 and vector2 are the two vectors for which we want to calculate the cosine similarity. The cosine() function returns a value ranging from 0 to 1, where 1 represents identical vectors, and 0 represents completely different vectors.
This approach considers the angle and magnitude of the vectors to measure their similarity, making it applicable in various domains, such as natural language processing, data mining, and recommendation systems.
For example:
from scipy import spatial
List1 = [4, 47, 8, 3]
List2 = [3, 52, 12, 16]
result = 1 - spatial.distance.cosine(List1, List2)
print(result)
Output:
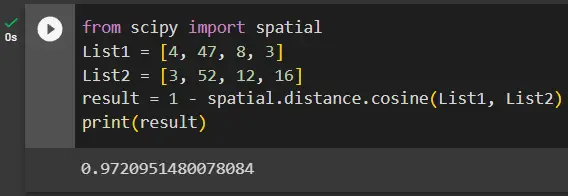
The above code calculates the cosine similarity between lists, List1 and List2, using the scipy.spatial.distance.cosine() function. The lists List1 and List2 are defined, containing numerical values.
The spatial.distance.cosine() function is then called with List1 and List2 as parameters, which calculates the cosine distance between the two lists. The returned value represents the dissimilarity between the lists.
The calculated distance is subtracted from 1 to obtain the cosine similarity instead. The result is stored in the variable result and finally printed.
Use the numpy Library to Calculate the Cosine Similarity in Python
Python’s numpy library provides powerful array operations, making it suitable for computing cosine similarity. To calculate cosine similarity using NumPy, we can leverage the np.dot() and np.linalg.norm() functions.
The numpy.dot() function takes two input arrays or matrices and computes their dot product. It performs element-wise multiplication and then sums the results. The output is a scalar value representing the dot product of the input arrays/matrices.
The numpy.norm() function takes an input array or matrix and computes its norm or magnitude. It calculates the square root of the sum of squared elements along the specified axis or the flattened array. The output is a scalar value representing the norm or magnitude of the input array or matrix.
We can use these functions with the correct formula to calculate the cosine similarity.
For example:
from numpy import dot
from numpy.linalg import norm
List1 = [4, 47, 8, 3]
List2 = [3, 52, 12, 16]
result = dot(List1, List2) / (norm(List1) * norm(List2))
print(result)
Output:
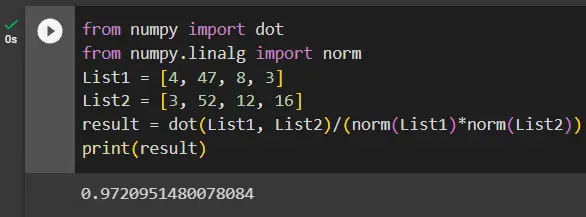
The above code calculates the cosine similarity between lists, List1 and List2, using the dot() function from the numpy library and the norm() function from the numpy.linalg module.
The dot() function computes the dot product between List1 and List2, representing the sum of the element-wise products of the two lists. The norm() function calculates a vector’s Euclidean norm or magnitude.
The formula dot(List1, List2) numerator calculates the dot product of the two lists. The denominator (norm(List1) * norm(List2)) calculates the product of their magnitudes.
Dividing the dot product by the product of the magnitudes gives the cosine similarity. The result is stored in the variable result and then printed.
We can use the following code if there are multiple or a list of vectors and a query vector to calculate cosine similarities.
import numpy as np
List1 = np.array([[4, 45, 8, 4], [2, 23, 6, 4]])
List2 = np.array([2, 54, 13, 15])
similarity_scores = List1.dot(List2) / (
np.linalg.norm(List1, axis=1) * np.linalg.norm(List2)
)
print(similarity_scores)
Output:
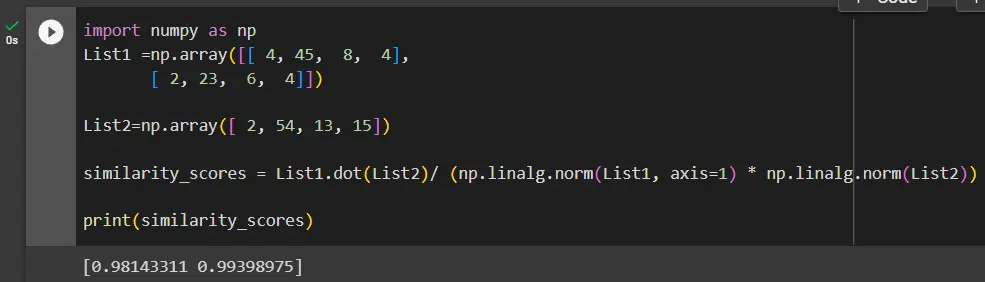
The above code calculates the cosine similarity scores between a matrix List1 and a vector List2 using the numpy library.
The List1.dot(List2) performs matrix multiplication between List1 and List2. The denominator (np.linalg.norm(List1, axis=1) * np.linalg.norm(List2)) calculates the product of the row-wise magnitudes of List1 and the magnitude of List2.
The resulting similarity scores are stored in the similarity_scores variable and printed. This code efficiently calculates the cosine similarity between a matrix and a vector.
Use the sklearn Library to Calculate the Cosine Similarity in Python
Python’s sklearn library provides a wide range of machine learning tools, including functions for calculating cosine similarity. To calculate cosine similarity using sklearn, we can utilize the cosine_similarity() function from the sklearn.metrics.pairwise module.
Syntax:
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity_matrix = cosine_similarity(vector1, vector2)
In this syntax, vector1 and vector2 are the two vectors for which we want to calculate the cosine similarity. The function returns a similarity matrix representing the two vectors’ cosine similarity.
The cosine_similarity() function measures the cosine similarity between two vectors by considering their magnitudes and angles. It is particularly useful in document similarity analysis, clustering, and recommendation systems.
See the code below.
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity, cosine_distances
A = np.array([10, 3])
B = np.array([8, 7])
result = cosine_similarity(A.reshape(1, -1), B.reshape(1, -1))
print(result)
Output:
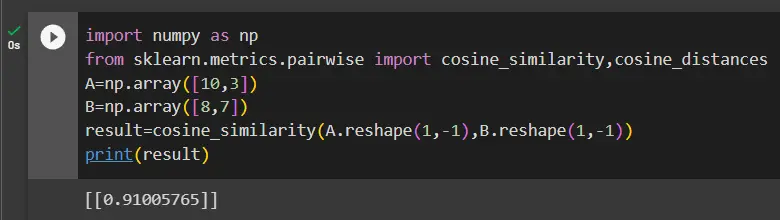
The above code calculates the cosine similarity between vectors A and B, using the cosine_similarity() function from the sklearn.metrics.pairwise module in scikit-learn.
First, the numpy arrays A and B are defined. To ensure proper shape for the calculation, A and B are reshaped using the reshape() function.
The cosine_similarity() function is then called with the reshaped vectors as parameters. It computes the cosine similarity between the vectors and returns a similarity matrix.
The resulting cosine similarity score is stored in the variable result and printed it.
Use the torch Module to Calculate the Cosine Similarity in Python
Python’s torch module provides powerful functionalities for deep learning and numerical computing, including functions for calculating cosine similarity. To compute cosine similarity using torch, we can utilize the torch.nn.functional.cosine_similarity() function.
Syntax:
import torch
cosine_similarity = torch.nn.functional.cosine_similarity(
tensor1, tensor2, dim=0, eps=1e-8
)
In this syntax, tensor1 and tensor2 are the input tensors for which we want to calculate the cosine similarity. The dim parameter specifies the dimension along which the cosine similarity is calculated. The eps parameter is used to prevent division by zero.
The cosine_similarity() function calculates the cosine similarity between the tensors by considering their magnitudes and angles. It returns a tensor containing the cosine similarity values. This functionality is widely used in applications like image similarity, text analysis, and recommendation systems.
See the code below.
import torch
import torch.nn.functional as F
t1 = [3, 45, 6, 8]
a = torch.FloatTensor(t1)
t2 = [4, 54, 3, 7]
b = torch.FloatTensor(t2)
result = F.cosine_similarity(a, b, dim=0)
print(result)
Output:
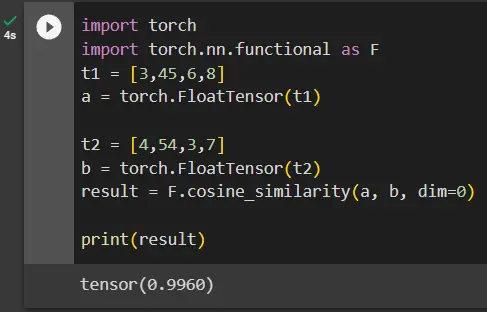
The above code calculates the cosine similarity between two tensors, a and b, using the cosine_similarity() function from the torch.nn.functional module in PyTorch.
First, two lists, t1 and t2, are defined. Then, these lists are converted to PyTorch tensors using torch.FloatTensor().
The cosine_similarity() function is then called with the tensors a and b as parameters and the dim argument set to 0. This computes the cosine similarity between the tensors along the specified dimension.
The resulting cosine similarity score is stored in the variable result and printed it.
Conclusion
Using different libraries, we have explored multiple methods to calculate cosine similarity in Python. Let’s compare the discussed approaches and their respective advantages and disadvantages.
The scipy.spatial.distance.cosine() function offers a straightforward method for calculating cosine similarity. It is easy to use and provides accurate results. However, it may be less efficient for large-scale computations due to its general-purpose nature.
The numpy.dot() and numpy.linalg.norm() functions provide efficient array operations for cosine similarity calculations. Numpy’s vectorized operations make it a suitable choice for handling large datasets. However, it requires more manual manipulation of arrays and reshaping.
For calculations involving string comparison, you can refer to how to compare strings using Python’s built-in capabilities in the article How to Compare Strings in Python.
The sklearn.metrics.pairwise.cosine_similarity() function provides a high-level and intuitive implementation for cosine similarity. It offers additional features like computing similarity matrices. However, it might involve some overhead when importing the sklearn library for just cosine similarity calculations.
The torch.nn.functional.cosine_similarity() function in the torch module benefits deep learning applications. It integrates well with other torch functionalities and provides GPU acceleration. However, it requires the installation of PyTorch and may be more suitable for scenarios involving neural networks and tensor operations.
For general-purpose cosine similarity calculations, the scipy or numpy libraries can be used for simplicity and efficiency. If working on larger datasets or requiring advanced features like similarity matrices, sklearn is a good choice.
The torch library is recommended in deep learning or neural network applications, where GPU acceleration is advantageous.
Ultimately, the choice of method depends on the specific requirements of the task at hand, the size of the data, and the overall project ecosystem.