How to Calculate the Confidence Interval Using SciPy

This article aims to help you calculate the confidence intervals in Python using SciPy. Before we dive into the calculation part, some basic information about the confidence interval needs to be understood.

Calculate the Confidence Interval Using SciPy

When we measure something, we must always calculate the degree of uncertainty in the outcome. Confidence intervals are a highly important tool for calculating a range within which we may locate the true value of an observable with a high degree of certainty.

Assume you inquire about one’s height. One could tell you that he’s 1.55 meters tall, but that doesn’t tell you anything about the uncertainty of this measurement.

Confidence intervals are intervals in which we have a high confidence level in determining the true value of the observable being measured. Scientists often want a 95% confidence interval, but 90% or even 99% is also frequent.

So, if you ask for the height, one should give you an estimate or a confidence interval, such as with 95% confidence, one has a height between 1.50 meters and 1.60 meters tall.

This tool provides us with an interval for determining the true value of the observable.

To calculate the confidence interval, we have to use the following formula:

Where:

• The x_bar is the sample mean.
• The z is the confidence level value.
• The n is the sample size.
• The s is the sample standard deviation.

Suppose we are working on data having a sample of less than 30; then, it is called a t-distribution. And to calculate its confidence interval, we will use the t.interval() function from the scipy.stats library.

Suppose we have datasets of the population in different villages. In this example, we will use a data set of size (n=23) to calculate the 95% confidence intervals using the t-distribution and the t.interval() method in Python, with the confidence parameter set to 0.95.

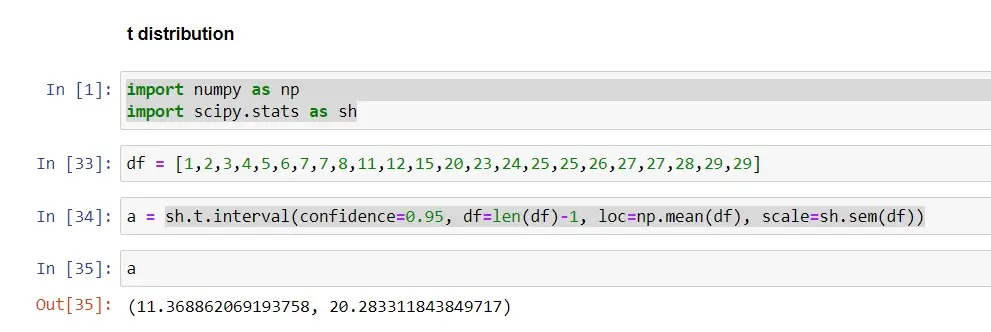
Here, you can see that t.interval() takes the parameters: confidence, data (df), loc (location parameter), and scale.

Let’s see the difference in confidence level when we use 99%.

When we use a 95% confidence interval, the interval is (11.37-20.28), whereas when we use a 99% confidence interval, the interval is (9.77-21.88). When comparing both intervals, we can see that the interval is wider when we use a CI of 99%, which means there is a 99% chance that the interval (9.77-21.88) contains the true population.

What should we do when we have a dataset of a sample size greater than 30? We can use the scipy.stats library’s norm.interval() method to obtain the confidence interval for a population mean of a given dataset when the dataset is normally distributed in Python.

In this example, we will use a random data set of size (n=60) to calculate the 95% confidence intervals using the normal distribution and the norm.interval() method in Python, with the alpha parameter set at 0.95.

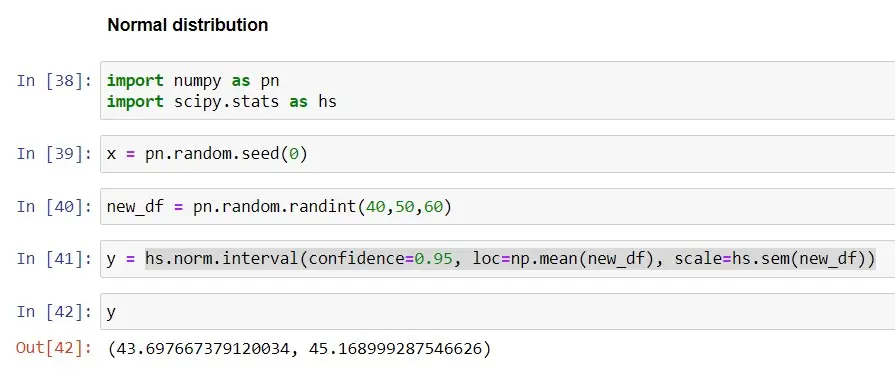
Let’s see the difference in confidence level when we use 99%.

When we use a 95% confidence interval, the interval is (43.70-45.17); when we use a 99% confidence interval, the interval is (43.47-45.41). When comparing both intervals, we can see that the interval is wider when we use a CI of 99%, which means there is a 99% chance that the interval (43.47-45.41) contains the true population.

Confidence intervals are simple to compute and can provide data analysts and scientists with valuable information. They provide a very powerful error estimate and, when applied appropriately, can truly help us extract as much information from our data as possible.