Linked List

1. Linked List over Array?
2. Linked List Traversal Algorithm
3. Linked List Traversal Illustration
4. Linked List Traversal Implementation
5. Linked List Traversal Algorithm Complexity

A linked list is a linear data structure. It is a collection of objects defined as nodes. But in the linked list, nodes are stored in random positions in memory and not stored in contiguous locations.

A node of the linked list consists of:

• A data item.

• An address of the next node.

class Node {
  int data;
  Node *next;
};

This representation of the node is used to create every node in the list. The data field stores the element, and *next is a pointer to store the next node’s address.

The address of the first node is called the head, and the last node is called the tail. The last node in the linked list points to NULL. So, when the list is empty head node points to the NULL node. Linked lists do not require declaring the size beforehand and can grow dynamically in size. It is very easy to insert and delete elements in a linked list. We do not need to move all the elements; only changing the previous and next elements’ pointers is sufficient.

Linked List over Array?

Linked lists have a natural advantage over array in the sense that we do not have to allocate a huge chunk of memory beforehand, but that also makes them cache unfriendly as memory is not allocated continuously. They allow easy insertion and deletion of elements with the help of pointers but also costs double memory for each node due to the space required by pointers. Linked lists also do not provide random access to elements. So, it is clear that there is no single winner and both linked lists and array have their own set of advantages and disadvantages.

Arrays should be used when we have a small list with knowledge of the maximum number of elements that we might store, whereas Linked lists should be used when there is a large list that is regularly changing.

Linked List Traversal Algorithm

Let the head be the first node of the linked list.

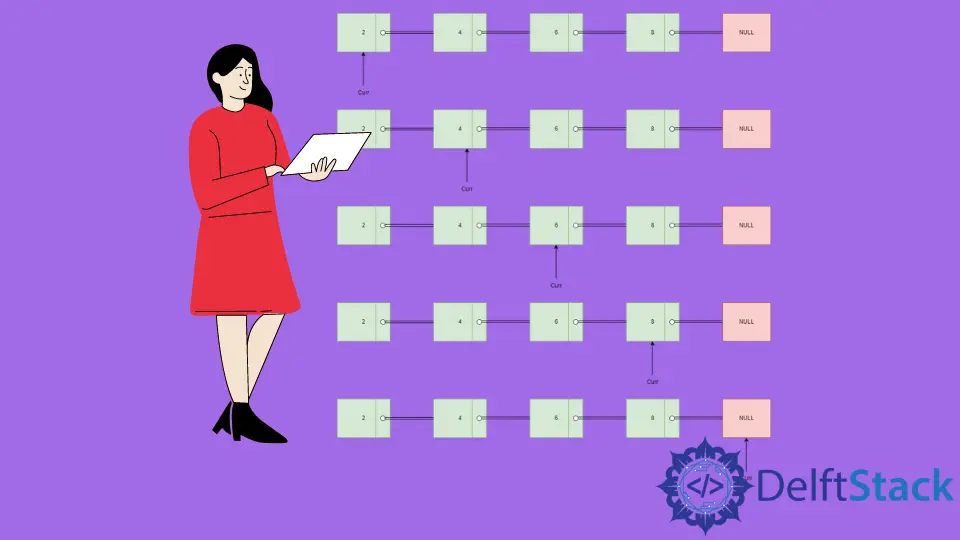
Linked List Traversal Illustration

Linked List Traversal Implementation

#include <bits/stdc++.h>
using namespace std;

class Node {
 public:
  int data;
  Node* next;
  Node(int x) {
    this->data = x;
    this->next = NULL;
  }
};

void printList(Node* head) {
  Node* curr = head;
  while (curr != NULL) {
    cout << curr->data << " ";
    curr = curr->next;
  }
}

int main() {
  Node* head = new Node(1);
  head->next = new Node(2);
  head->next->next = new Node(3);
  head->next->next->next = new Node(4);
  head->next->next->next->next = new Node(5);
  head->next->next->next->next->next = new Node(6);
  printList(head);
  return 0;
}

Linked List Traversal Algorithm Complexity

Time Complexity

• Average Case

To traverse the complete linked list, we have to visit each node. So, if a linked list has n nodes, the average-case time complexity of traversal is of the order of O(n). The time complexity is of the order of O(n).

• Best Case

The best-case time complexity is O(n). It is the same as average-case time complexity.

• Worst Case

The worst-case time complexity is O(n). It is the same as best-case time complexity.

Space Complexity

This traversal algorithm’s space complexity is O(1) as no extra space other than the curr pointer is required.