Linked List Insertion

1. Linked List Insertion Algorithm
2. Linked List Insertion Illustration
3. Linked List Insertion Implementation
4. Linked List Insertion Algorithm Complexity

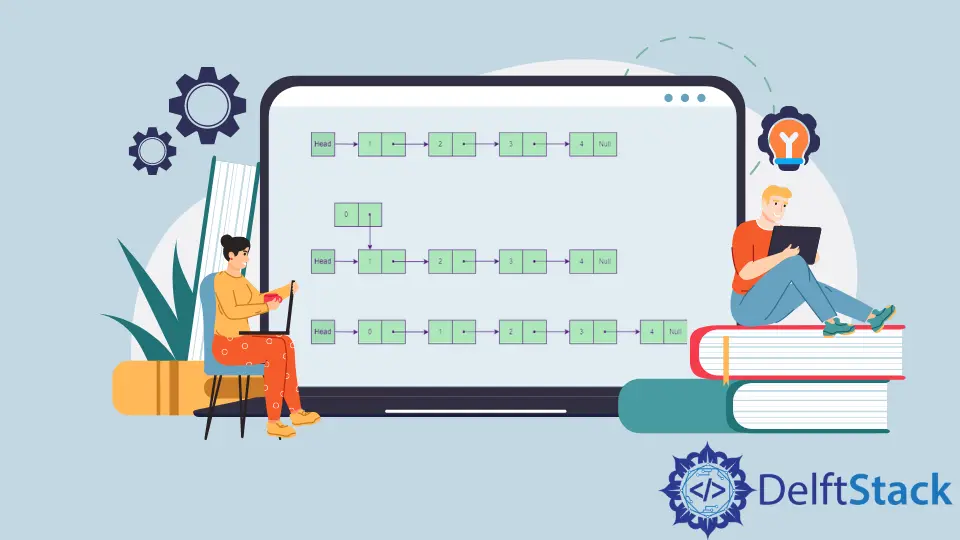
In this article, we will learn how to insert a node in a linked list. We can see that 4 different scenarios arise.

1. We want to insert a node before the head of the linked list. This operation resembles the push operation in the stack.
2. We want to insert a node at the end of the linked list i.e. next to the tail node.
3. We want to insert a node at the i-th position of the linked list.
4. We have the reference of the node, after which we want to insert the new node.

Linked List Insertion Algorithm

Let the head be the pointer to the first node of the linked list and let x be the data to be inserted into the linked list.

Insert Node at the Head of the Linked List push()

Insert Node at the End of the Linked List append()

Insert Node at the i-th Position of the Linked List insertNpos()

Insert Node Next to Reference of Given Node insertAfter()

Linked List Insertion Illustration

Assume that we have a node temp with a data value equal to 5 and we want to insert it in the linked list. Let us consider all 4 cases and illustrate how the above algorithms work.

Insert Node at the Head of the Linked List push()

Insert Node at the End of the Linked List append()

Insert Node at the i-th Position of the Linked List insertNpos()

We will insert our node at position 3.

Insert Node Next to Reference of Given Node insertAfter()

Linked List Insertion Implementation

#include <bits/stdc++.h>
using namespace std;

class Node {
 public:
  int data;
  Node* next;
  Node(int x) {
    this->data = x;
    this->next = NULL;
  }
};

void push(Node** head, int x) {
  Node* temp = new Node(x);
  temp->next = (*head);
  (*head) = temp;
}

void insertAfter(Node* prev, int x) {
  if (prev == NULL) {
    return;
  }
  Node* curr = new Node(x);
  curr->next = prev->next;
  prev->next = curr;
}

void printList(Node* head) {
  Node* curr = head;
  while (curr != NULL) {
    cout << curr->data << " ";
    curr = curr->next;
  }
}
void insertNpos(Node** head, int x, int pos) {
  if (pos <= 0) {
    return;
  }
  if (!head && pos == 1) {
    *head = new Node(x);
  } else if (pos == 1) {
    push(head, x);
  }
  Node* temp = new Node(x);
  Node* curr = *head;
  while (pos--) {
    if (pos == 1) {
      if (curr) {
        temp->next = curr->next;
        curr->next = temp;
      }
      return;
    }
    curr = curr->next;
  }
}
void append(Node** head, int x) {
  Node* temp = new Node(x);
  Node* tail = *head;
  if (*head == NULL) {
    *head = temp;
    return;
  }
  while (tail->next != NULL) tail = tail->next;
  tail->next = temp;
  return;
}

int main() {
  Node* head = new Node(1);
  head->next = new Node(2);
  printList(head);
  cout << "\n";
  push(&head, 3);
  push(&head, 4);
  printList(head);
  cout << "\n";
  append(&head, 5);
  printList(head);
  cout << "\n";
  insertAfter(head->next->next, 6);
  printList(head);
  cout << "\n";
  insertNpos(&head, 24, 2);
  printList(head);
  return 0;
}

Linked List Insertion Algorithm Complexity

Time Complexity

• Average Case

To insert a node at the i-th position in the linked list, we have to visit i nodes. So, the time complexity is of the order of O(i). And we have n nodes in the linked list, so on the average-case time complexity is O(n/2) or O(n). The time complexity is of the order of O(n).

• Best Case

The best-case occurs when we want to insert a node at the head of the linked list or we have the reference to the node before the site of insertion. The best-case time complexity is O(1).

• Worst Case

The worst-case time complexity is O(n). It is the same average-case time complexity.

Space Complexity

This insertion algorithm’s space complexity is O(1) as no extra space other than curr pointer is required.