Linked List Reversal

  2. Tutorial
  3. Data Structure
  4. Linked List Reversal
Harshit Jindal Feb 15, 2024
Data Structure Linked List
  1. Linked List Reversal Algorithm
  2. Linked List Reversal Illustration
  3. Linked List Reversal Implementation
  4. Linked List Reversal Algorithm Complexity
Linked List Reversal

A linked list is a linear data structure. A node of the linked list consists of:

  • A data item.
  • An address of the next node.
class Node {
  int data;
  Node *next;
};

linked list

This article will introduce how to reverse a linked list given the pointer to the head node of the linked list.

Linked List Reversal Algorithm

Let the head be the first node of the linked list.

Iterative Algorithm

  • Initialize 3 pointers - curr as head, prev and next as NULL.
  • Traverse the linked list until you reach the last node i.e. curr != NULL and do the following:
    • Set next as curr->next to move next to its next node.
    • Reverse current node’s direction by pointing them toward prev. So, set curr->next as prev
    • Set prev as curr to move it one position ahead.
    • Set curr as next to move it one position ahead.

Recursive Algorithm

  • Divide the list into two parts: the first node, i.e., the head node, and the rest of the linked list.
  • Call reverse(head->next), i.e., reverse the rest of the linked list and store the reversed linked list as rev.
  • Append head to the end of the reversed linked list rev.

Reverse Linked List Using Stack

  • Initialize pointer curr to the head of the linked list.
  • Traverse the linked list and insert each node in the stack one by one.
  • Update head to the last node in the linked list i.e. the first node in the stack.
  • Start popping the nodes out of the stack one by one and append it to the end of reversed linked list.
  • Update the next pointer of the last node to NULL.

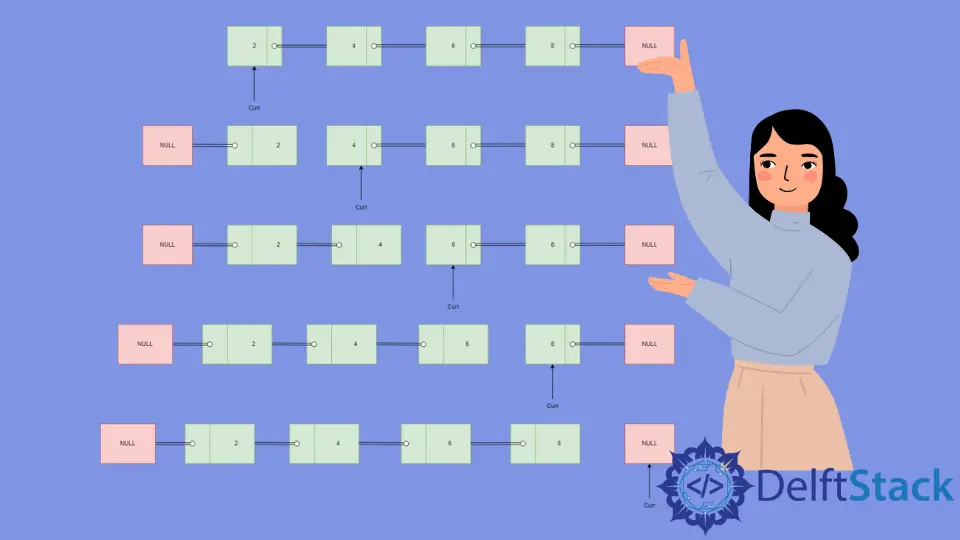
Linked List Reversal Illustration

linked list reversal

  • Initialize curr to point towards head i.e. node with data 2 and prev and curr as NULL.
  • Point next to curr->next with a value equal to 4.
  • Set curr->next as prev to get a reversed linked list with 2 as the head.
  • Move prev to curr i.e. node with data as 2 and curr to next i.e. node with data as 4.
  • Point next to curr->next with a value equal to 6.
  • Set curr->next as prev to get a reversed linked list with 2 and 4 as reversed nodes with 4 as the head.
  • Move prev to curr i.e. node with data as 4 and curr to next i.e. node with data as 6.
  • Point next to curr->next with a value equal to 8.
  • Set curr->next as prev to get a reversed linked list with 2, 4, and 6 as reversed nodes with 6 as the head.
  • Move prev to curr i.e. node with data as 6 and curr to next i.e. node with data as 8.
  • Point next to curr->next which is NULL.
  • Set curr->next as prev to get a reversed linked list with 2, 4, 6, and 8 as reversed nodes with 8 as the head.
  • Move prev to curr i.e. node with data as 8 and curr to NULL and the algorithm terminates.

Linked List Reversal Implementation

#include <bits/stdc++.h>
using namespace std;

class Node {
 public:
  int data;
  Node* next;
  Node(int x) {
    this->data = x;
    this->next = NULL;
  }
};

void printList(Node* head) {
  Node* curr = head;
  while (curr != NULL) {
    cout << curr->data << " ";
    curr = curr->next;
  }
}

Node* reverse(Node* head) {
  Node* curr = head;
  Node *prev = NULL, *next = NULL;

  while (curr != NULL) {
    next = curr->next;
    curr->next = prev;
    prev = curr;
    curr = next;
  }
  head = prev;
  return head;
}

Node* recursiveReverse(Node* head) {
  if (head == NULL || head->next == NULL) return head;

  Node* rest = recursiveReverse(head->next);
  head->next->next = head;
  head->next = NULL;
  return rest;
}

void reverseLL(Node** head) {
  stack<Node*> s;
  Node* temp = *head;
  while (temp->next != NULL) {
    s.push(temp);
    temp = temp->next;
  }
  *head = temp;

  while (!s.empty()) {
    temp->next = s.top();
    s.pop();
    temp = temp->next;
  }
  temp->next = NULL;
}

int main() {
  Node* head = new Node(1);
  head->next = new Node(2);
  head->next->next = new Node(3);
  head->next->next->next = new Node(4);
  head->next->next->next->next = new Node(5);
  head->next->next->next->next->next = new Node(6);
  head = reverse(head);
  printList(head);
  cout << "\n";
  head = recursiveReverse(head);
  printList(head);
  cout << "\n";
  reverseLL(&head);
  printList(head);
  cout << "\n";
  return 0;
}

Linked List Reversal Algorithm Complexity

Time Complexity

  • Average Case

To reverse the complete linked list, we have to visit every node and then append it to reversed list. So, if a linked list has n nodes, the average-case time complexity of traversal is of the order of O(n). The time complexity is of the order of O(n).

  • Best Case

The best-case time complexity is O(n). It is the same as average-case time complexity.

  • Worst Case

The worst-case time complexity is O(n). It is the same as best-case time complexity.

Space Complexity

This traversal algorithm’s space complexity is O(1) as no extra space other than for temporary pointers is required.

Author: Harshit Jindal
Harshit Jindal avatar Harshit Jindal avatar

Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.

LinkedIn

Related Article - Data Structure

Related Article - Linked List