Binary Tree Traversal

1. Binary Tree Traversal
2. Binary Tree Traversal Illustration
3. Binary Tree Traversal Algorithm
4. Binary Tree Traversals Implementation
5. Binary Tree Traversal Algorithm Complexity

A Binary Tree is a non-linear data structure. It is called a binary tree because each node has a maximum of two children. These children are called left children and right children. It can also be interpreted as an undirected graph in which the topmost node is called root. Unlike linear data structures that can only be traversed in only one way, a tree can be traversed in different ways. We can traverse a tree by exploring along the depth or the breadth. The first approach is called the Depth-First Traversal, and the second is called the Breadth-First Traversal. In this article, we will discuss the Depth-First Traversals.

There are 3 kinds of depth-first traversals - inorder, preorder, and postorder. We will discuss each of them one by one.

Binary Tree Traversal

Inorder Traversal

In this traversal, we first visit the left subtree, then the root, and lastly the right subtree. Every node resembles a subtree. For BST, inorder traversal returns all the elements in ascending order

Preorder Traversal

In this traversal, we first visit the root, then the left subtree, and lastly the right subtree. Every node resembles a subtree. It is normally used to replicate, i.e., create a copy of the tree. Prefix traversal also helps to generate prefix expression from an expression tree.

Postorder Traversal

In this traversal, we first visit the left subtree, then the right subtree, and lastly the root. Every node resembles a subtree. It is used to delete trees effectively. It also helps to generate postfix expression from an expression tree.

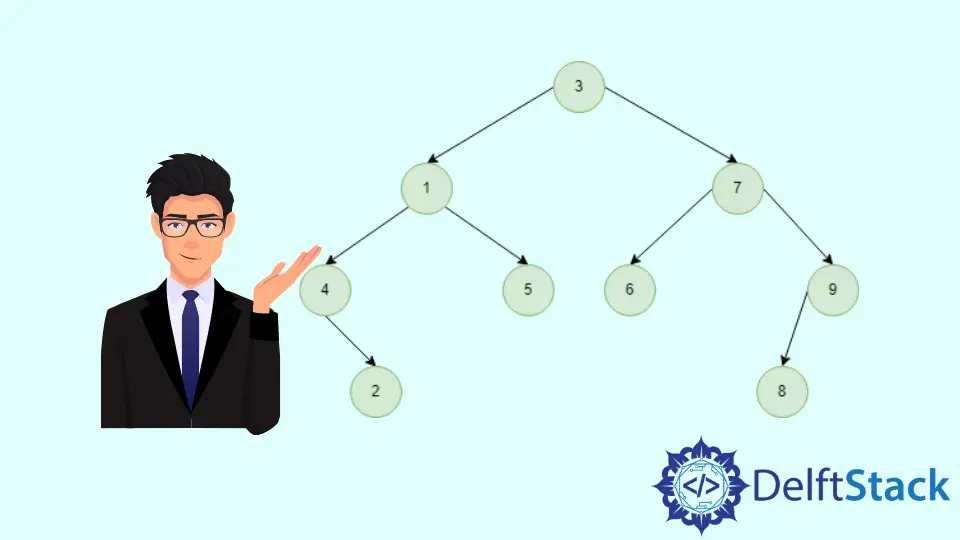
Binary Tree Traversal Illustration

Inorder Traversal: (4, 2, 1, 5, 3, 6, 7, 8, 9)

We call inorder traversal on root node 3. Recursively traverse left to reach node 4, which is the leftmost node, and include it in our output; as it is the root and has no left node, we visit its rightmost node 2 and include it in our traversal. In this way, we traverse the whole tree to get the above order as our output.

Preorder Traversal: (3, 1, 4, 2, 5, 7, 6, 9, 8)

We call preorder traversal on root node 3 and include it in our output. Then we recursively traverse left to reach the next root node 1 and then subsequently 4. Since 4 has no left child, we visit the right node 2. Now we have covered the subtree under the root node 4 and we trace back to node 1 and go towards its right to node 5. This way, we traverse the whole tree to get the above order as our output.

Postorder Traversal: (2, 4, 5, 1, 6, 8, 9, 7, 3)

We call postorder traversal on root node 3.Recursively traverse left to reach node 4. Before including 4 in our traversal, we have to visit its right node 2. We include 2 and then 4 in our output and move back to 1.1 has its right node 5 unvisited, so we first include 5 and then 1 in output. Then we trace back to root node 3 and proceed with traversing the right subtree. This way, we traverse the whole tree to get the above order as our output.

Binary Tree Traversal Algorithm

Inorder Traversal

Preorder Traversal

Postorder Traversal

Binary Tree Traversals Implementation

#include <iostream>
using namespace std;

class Node {
 public:
  int key;
  Node *left, *right;
  Node(int x) {
    this->key = x;
    this->left = this->right = NULL;
  }
};

void inorder(Node* root) {
  if (root != NULL) {
    inorder(root->left);
    cout << root->key << " ";
    inorder(root->right);
  }
}
void preorder(Node* root) {
  if (root != NULL) {
    cout << root->key << " ";
    preorder(root->left);
    preorder(root->right);
  }
}

void postorder(Node* root) {
  if (root != NULL) {
    postorder(root->left);
    postorder(root->right);
    cout << root->key << " ";
  }
}

int main() {
  Node* root = new Node(3);
  root->left = new Node(1);
  root->right = new Node(7);
  root->left->left = new Node(4);
  root->left->right = new Node(5);
  root->left->left->right = new Node(2);
  root->right->left = new Node(6);
  root->right->right = new Node(9);
  root->right->right->left = new Node(8);
  cout << "The inorder traversal of the tree is : ";
  inorder(root);
  cout << endl;
  cout << "The preorder traversal of the tree is : ";
  preorder(root);
  cout << endl;
  cout << "The postorder traversal of the tree is : ";
  postorder(root);
  cout << endl;
}

Binary Tree Traversal Algorithm Complexity

Time Complexity

• Average Case

There are n nodes in a tree, in all 3 kinds of traversals, we have to go and visit each node. Since we iterate over n nodes, although in a different order, the time complexity for all 3 traversals is the order of O(n). The average-case time complexity is O(n).

• Best Case

The best-case time complexity is O(n). It is the same as average-case time complexity for all the 3 traversals.

• Worst Case

The worst-case time complexity is O(n). It is the same as worst-case time complexity for all the 3 traversals.

Space Complexity

The algorithm’s space complexity is O(n) due to the extra space required by recursion calls.