Convert Binary Tree to Binary Search Tree

1. Algorithm of Converting Binary Tree to BST
2. Convert Binary Tree to BST Illustration
3. Convert Binary Tree to BST Implementation
4. Convert Binary Tree to BST Algorithm Complexity

A Binary Tree is a non-linear data structure. It is called a binary tree because each node has a maximum of two children. These children are called left children and right children. It can also be interpreted as an undirected graph in which the topmost node is called root. A Binary Search Tree (BST) is a binary tree with special properties that helps to keep the data organized in a sorted fashion.

In this tutorial, we will discuss how to convert a binary tree to BST while maintaining the Binary Tree’s original structure.

Algorithm of Converting Binary Tree to BST

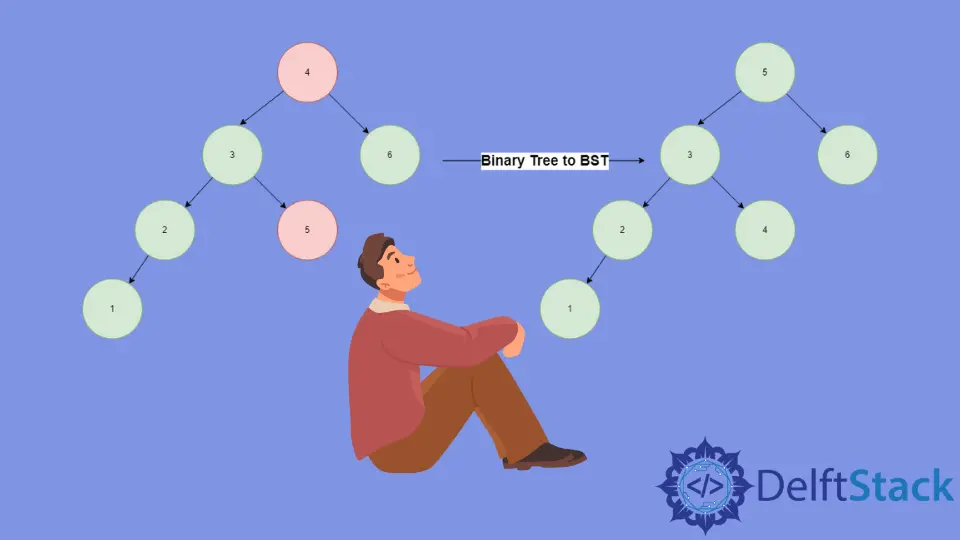
Convert Binary Tree to BST Illustration

Convert Binary Tree to BST Implementation

#include <bits/stdc++.h>
using namespace std;

class Node {
 public:
  int data;
  Node *left, *right;
  Node(int x) {
    this->data = x;
    this->left = this->right = NULL;
  }
};
vector<int> v;

void inorder(Node* root) {
  if (root != NULL) {
    inorder(root->left);
    cout << root->data << " ";
    inorder(root->right);
  }
}

void storetree(Node* root, int i = 0) {
  if (!root) {
    return;
  }
  storetree(root->left);
  v.push_back(root->data);
  storetree(root->right);
}

void restoretree(Node* root, int& i) {
  if (!root) {
    return;
  }
  restoretree(root->left, i);
  root->data = v[i];
  i++;
  restoretree(root->right, i);
}

void converttoBST(Node* root) {
  if (!root) {
    return;
  }
  storetree(root);
  sort(v.begin(), v.end());
  int i = 0;
  restoretree(root, i);
}

int main() {
  Node* root = new Node(3);
  root->left = new Node(1);
  root->right = new Node(7);
  root->left->left = new Node(4);
  root->left->right = new Node(5);
  root->left->left->right = new Node(2);
  root->right->left = new Node(6);
  root->right->right = new Node(9);
  root->right->right->left = new Node(8);
  cout << "The inorder traversal of the tree is : ";
  inorder(root);
  cout << endl;
  converttoBST(root);
  cout << "The inorder traversal of the tree is : ";
  inorder(root);
  cout << endl;
}

Convert Binary Tree to BST Algorithm Complexity

Time Complexity

• Average Case

The time complexity of doing the inorder traversal in which we store the array in sorted and store the sorted array back to the binary tree is O(n). But, the complexity of sorting the array is O(nlogn) and hence the total complexity is given as O(nlogn) + 2*O(n). The time complexity is of the order of O(nlogn).

• Best Case

The best-case time complexity is of the order of O(n). When the given binary tree is already a BST, we do the inorder traversal to realize it, and no sorting operations are required.

• Worst Case

The worst-case time complexity is of the order of O(nlogn).

Space Complexity

The algorithm’s space complexity is O(n) due to the extra space required by recursion calls.