Sieve of Eratosthenes in Python

The Sieve of Eratosthenes is a very common algorithm to get the prime numbers below a given number. This number should be less than ten million.

The algorithm is simple to understand and is frequently implemented in programming. This tutorial will demonstrate implementing Python’s Sieve of Eratosthenes algorithm.

Let us begin by first understanding the logic behind this algorithm. First, we write all the numbers between 2 and the provided number Let us assume 50.

Then we take the first prime number, 2, and mark all the numbers greater than its square and divisible by 2. We then repeat the same with the next prime number, 3.

The same procedure is carried out until the prime number 7 square of the next number after 7 is 121 and greater than 50. After marking all the numbers, the unmarked values are the prime numbers till 50.

The figure below demonstrates the final result.

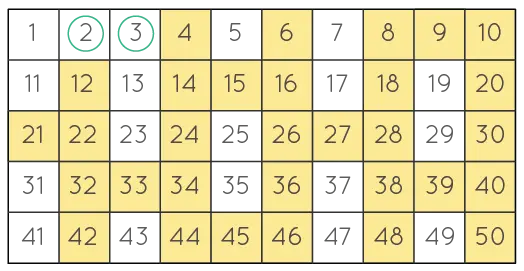
Use the Sieve of Eratosthenes in Python

We will first create a list of the required range. This list will mark True or False for the given index.

Initially, the list contains all elements as True. We will use a nested loop to make the changes and mark non-prime positions as False.

After this, we will store the positions where the value is still True in a new list. This list contains the prime numbers.

def sieve_of_eratosthenes(val):
    max = val + 1
    lst = [True] * max
    for i in range(2, int(val ** 0.5 + 1)):
        if lst[i]:
            for j in range(i * i, max, i):
                lst[j] = False
    final = []
    for i in range(2, max):
        if lst[i]:
            final.append(i)
    return final


print(sieve_of_eratosthenes(100))

Output:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

It is possible to make minor changes to the above code to improve the time complexity. For instance, we can use sets or dictionaries to filter non-prime numbers.

The final result is returned in a list, but use dictionaries or sets while marking the prime and non-prime numbers as True or False.

def sieveoferatosthenes_dict(n):
    max = n + 1
    d = dict()
    for i in range(2, max):
        d[i] = True

    for i in d:
        factors = range(i, max, i)
        for f in factors[1:]:
            d[f] = False
    lst = [i for i in d if d[i] == True]
    return lst


print(sieveoferatosthenes_dict(100))

Output:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

In the above example, we use the dictionary d for marking the values as True or False to filter out the prime numbers. The final result is in a list.