How to Implement Depth-First Search in Python

1. Depth First Search Example Using a Graph in Python
2. Depth First Search Using Recursion in Python
3. Depth First Search Using Iteration in Python

The depth-first search is an algorithm for traversing a tree or a graph. In DFS, traversing starts from the root node and goes deeper and deeper.

It performs backtracking and upward when it reaches the leaf node.

Depth First Search is used in many applications like:

• Detecting cycle in a graph
• Path Finding
• Travelling-Salesman Problem

Depth First Search Example Using a Graph in Python

We have six vertices, 1 is the root vertex. We will traverse 1, then it has two adjacent vertices 5 and 9, so first, we will traverse its left vertex, and then we will traverse the adjacent vertex of 5.

When finding a leaf node, we will backtrack and repeat the same procedure to recent unvisited nodes.

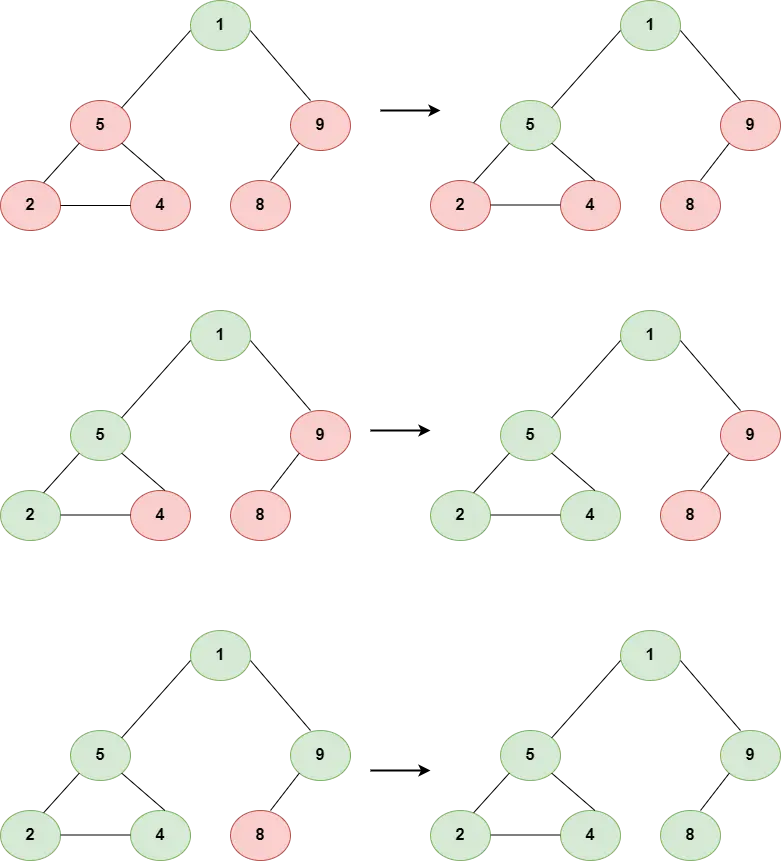
In this example, green vertices are the traversed ones, and red is the not yet traversed ones.

Depth First Search Using Recursion in Python

The recursion technique calls the DFS function. The base condition is true when traversing all the graph’s vertices.

The following code uses a dictionary data structure to represent an adjacency list to store a graph in memory.

We will declare a set to keep track of all the vertices we have visited.

If the vertex is not traversed, we traverse it first by printing it and adding it to the traversed set.

# Python 3.x
graph = {"1": ["5", "9"], "5": ["2", "4"], "9": ["8"], "2": ["4"], "4": ["2"], "8": []}
traversed = set()


def dfs(traversed, graph, vertex):
    if vertex not in traversed:
        print(vertex)
        traversed.add(vertex)
        for adjacent in graph[vertex]:
            dfs(traversed, graph, adjacent)


print("Depth First Search:")
dfs(traversed, graph, "1")

Output:

# python 3.x
Depth First Search:
1
5
2
4
9
8

We had to go deeper and deeper by traversing the adjacent vertex of the graph and performing DFS.

We backtracked, visited the most recent unvisited vertices, and performed DFS for that vertex.

In the driver code, we had to call the dfs function and specify the root vertex, 1 in our case.

Depth First Search Using Iteration in Python

Use a loop to iterate over the graph’s vertices. We will also use a stack to keep track of unvisited vertices.

First, we will traverse the root node and push it into the stack. Then while our stack is not empty, we will peek (read topmost most vertex without removing it) a vertex from the stack, and if that vertex is not traversed, we will traverse it.

Then we will read the adjacent vertex of the vertex we just traversed and push it into the stack if we have not traversed it before.

# Python 3.x
def dfs(graph, root_node):
    traversed = [root_node]
    stack = [root_node]
    while stack:
        vertex = stack[-1]
        if vertex not in traversed:
            traversed.extend(vertex)
        pop = True
        for adjacent in graph[vertex]:
            if adjacent not in traversed:
                stack.extend(adjacent)
                pop = False
                break
        if pop:
            stack.pop()
    return traversed


graph = {"1": ["5", "9"], "5": ["2", "4"], "9": ["8"], "2": ["4"], "4": ["2"], "8": []}
print(dfs(graph, "1"))

Output:

#python 3.x
['1', '5', '2', '4', '9', '8']

We had to go deeper and deeper and reach the leaf node with no adjacent vertices. We had pop leaf nodes from the stack because DFS will not be performed, and we have already traversed it.

So, the for loop does has not been executed. We will backtrack.

The control goes again in the while loop, and DFS performed for the peek element of the stack until the stack is empty.