Python Audio Synthesis
- Python Audio Synthesis
-
Use
IPython.displayfor Additive Synthesis in Python - Make Various Basic Wave Forms With Additive Synthesis in Python
-
Use
pyaudioto Generate Audio Synthesis in Python
Today, we will learn about audio synthesis and how we can generate sound using Python.
Python Audio Synthesis
Sound synthesis or audio synthesis generates sound electronically (using hardware or software) that mimics the human voice or musical instruments.
Synthesis is primarily for music, where an electronic device/instrument known as a synthesizer is used to record and perform music.
Now, the point is can we use Python to generate these kinds of simple sounds, for instance, sine wave? Do we have any module for that, or how can we create our own?
Let’s learn the different ways below.
Use IPython.display for Additive Synthesis in Python
-
First, we import the necessary modules and libraries. We import
IPythonto display sound player,numpyfor working with arrays,matplotlibfor plotting charts (we’ll be doing it while generating basic waveforms), andmathto use mathematical functions.import IPython.display as ipd import numpy import math import matplotlib.pyplot as plt -
Set the sample rate. Here, we set the
sample_ratewith22050.sample_rate = 22050 -
Make the sine waveform.
def makesine(frequency, duration): t = numpy.linspace(0, duration, math.ceil(sample_rate * duration)) x = numpy.sin(2 * numpy.pi * frequency * t) return xAt this step, we define a function
makesine(), which takesfrequencyanddurationas parameters. We usedurationinnumpy.linspace()andfrequencyinnumpy.sin()methods to reuse pure sine waveforms.Note that the
numpy.linspace()creates numeric sequences, or we can say it returns evenly spaced numbers/samples w.r.t. interval (start,stop). It is similar to thenumpy.arange()but takes a sample number (num) as a parameter instead ofstep.You can find more on that here.
On the other hand,
numpy.sin()calculates the trigonometric sine for all the specifiedx(an array of elements). -
Run
makesine().output = numpy.array(()) y = makesine(261.63, 0.5) # C for 0.5 seconds output = numpy.concatenate((output, y)) y = makesine(293.66, 0.5) # D for 0.5 seconds output = numpy.concatenate((output, y)) y = makesine(329.63, 0.5) # E for 0.5 seconds output = numpy.concatenate((output, y)) ipd.Audio(output, rate=sample_rate)Next, we execute
makesine()multiple times to form a new waveform with specifiedfrequencyandduration. After that, we usenumpy.concatenate()to place all of them together.You can find the complete working source code below with the respective output.
-
Here is the complete source code.
import IPython.display as ipd import matplotlib.pyplot as plt import numpy import math sample_rate = 22050 def makesine(frequency, duration): t = numpy.linspace(0, duration, math.ceil(sample_rate * duration)) x = numpy.sin(2 * numpy.pi * frequency * t) return x output = numpy.array(()) y = makesine(261.63, 0.5) # C for 0.5 seconds output = numpy.concatenate((output, y)) y = makesine(293.66, 0.5) # D for 0.5 seconds output = numpy.concatenate((output, y)) y = makesine(329.63, 0.5) # E for 0.5 seconds output = numpy.concatenate((output, y)) ipd.Audio(output, rate=sample_rate)OUTPUT:
Make Various Basic Wave Forms With Additive Synthesis in Python
We are done with the basic sine waveform. Let’s experiment with various basic waveforms with frequencies at the integer multiples using frequency * i; here, i is the counter from 1 and increments by 1 every time.
We need to soften these sine waves into predefined amplitudes (amplist), which are then stacked up in the output. To make that happen, we are required to make a function named addsyn() as follows:
def addsyn(frequency, duration, amplist):
i = 1
t = numpy.linspace(0, duration, math.ceil(sample_rate * duration))
output = numpy.zeros(t.size)
for amp in amplist:
x = numpy.multiply(makesine(frequency * i, duration), amp)
output = output + x
i += 1
if numpy.max(output) > abs(numpy.min(output)):
output = output / numpy.max(output)
else:
output = output / -numpy.min(output)
return output
Inside the addsyn(), we initialize a new output. Inside the for loop, we make the sine waveform with a maximum amplitude (amp); here, frequency is an integer multiple.
Then, we sum it to the output and save it in the output variable. Next, we ensure that the maximum amplitude doesn’t exceed 1 and return the output.
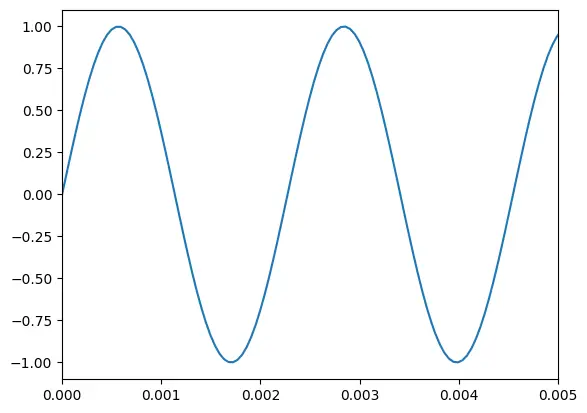
Now, we can execute the following piece of code to make only one harmonic sine wave and make a chart for it that shows only 0.005 seconds to see this waveform shape.
t = numpy.linspace(0, 1, sample_rate)
sinewave = addsyn(440, 1, [1])
plt.plot(t, sinewave)
plt.xlim(0, 0.005)
ipd.Audio(sinewave, rate=sample_rate)
The complete source code would be as follows.
Example Code:
import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy
import math
sample_rate = 22050
def addsyn(frequency, duration, amplist):
i = 1
t = numpy.linspace(0, duration, math.ceil(sample_rate * duration))
output = numpy.zeros(t.size)
for amp in amplist:
x = numpy.multiply(makesine(frequency * i, duration), amp)
output = output + x
i += 1
if numpy.max(output) > abs(numpy.min(output)):
output = output / numpy.max(output)
else:
output = output / -numpy.min(output)
return output
t = numpy.linspace(0, 1, sample_rate)
sinewave = addsyn(440, 1, [1])
plt.plot(t, sinewave)
plt.xlim(0, 0.005)
ipd.Audio(sinewave, rate=sample_rate)
OUTPUT:
python audio synthesis - basic sine waveform harmonic.wav
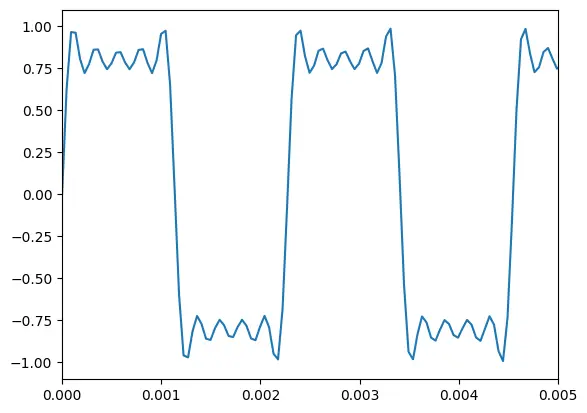
Now, we can play around with different values of the addsyn() function to get different outputs. See another example to create a square wave below.
Example Code:
import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy
import math
sample_rate = 22050
def addsyn(frequency, duration, amplist):
i = 1
t = numpy.linspace(0, duration, math.ceil(sample_rate * duration))
output = numpy.zeros(t.size)
for amp in amplist:
x = numpy.multiply(makesine(frequency * i, duration), amp)
output = output + x
i += 1
if numpy.max(output) > abs(numpy.min(output)):
output = output / numpy.max(output)
else:
output = output / -numpy.min(output)
return output
t = numpy.linspace(0, 1, sample_rate)
square_wave = addsyn(440, 1, [1, 0, 0.349, 0, 0.214, 0, 0.156, 0, 0.121, 0])
plt.plot(t, square_wave)
plt.xlim(0, 0.005)
ipd.Audio(square_wave, rate=sample_rate)
OUTPUT:
python audio synthesis - basic sine waveform square.wav
Use pyaudio to Generate Audio Synthesis in Python
Here, we will use pyaudio, a Python module recording audio with Python.
-
First, we import necessary libraries:
mathfor performing mathematical functions andpyaudiofor generating waves.import math # import needed modules import pyaudio # sudo apt-get install python-pyaudio -
Initialize
pyaudio.PyAudio = pyaudio.PyAudio -
Initialize variables.
bit_rate = 16000 frequency = 500 length = 1 bit_rate = max(bit_rate, frequency + 100) number_of_frames = int(bit_rate * length) rest_frames = number_of_frames % bit_rate wave_data = ""Here, we initialized the
bit_ratewith16000, which shows the number of frames per second. Thefrequencyis set to500Hz denoting the waves per second (261.63=C4-note) whilelengthis initialized with1.After that, we use the
max()function to find the maximum frombit_rateandfrequency+100and assign the maximum value tobit_rate. Then, we multiply thebit_rateandlength, convert it tointtype using theint()function and assign it tonumber_of_frames.Next, we use the modulo operator (
%) to dividenumber_of_frameswithbit_rateand assign the remainder torest_frames. Finally, we initializewave_datawith an empty string. -
Generate waves.
for x in range(number_of_frames): wave_data = wave_data + chr( int(math.sin(x / ((bit_rate / frequency) / math.pi)) * 127 + 128) ) for x in range(rest_frames): wave_data = wave_data + chr(128)Here, we used two
forloops that iterate until thenumber_of_framesto generate waves. -
Record audio.
p = PyAudio() stream = p.open( format=p.get_format_from_width(1), channels=1, rate=bit_rate, output=True ) stream.write(wave_data) stream.stop_stream() stream.close() p.terminate()Here, we created an instance of
PyAudio, saved the reference inp, and used that reference to open a stream using theopen()method, which will record audio. Next, we wrotewave_data, stopped the stream, and closed it. Finally, terminate thePyAudioinstance (p) as well.You can read about
open(),write(),stop_stream(), andclose()here in detail. -
Here is the complete source code.
import math import pyaudio PyAudio = pyaudio.PyAudio bit_rate = 16000 frequency = 500 length = 1 bit_rate = max(bit_rate, frequency + 100) number_of_frames = int(bit_rate * length) rest_frames = number_of_frames % bit_rate wave_data = "" for x in range(number_of_frames): wave_data = wave_data + chr( int(math.sin(x / ((bit_rate / frequency) / math.pi)) * 127 + 128) ) for x in range(rest_frames): wave_data = wave_data + chr(128) p = PyAudio() stream = p.open( format=p.get_format_from_width(1), channels=1, rate=bit_rate, output=True ) stream.write(wave_data) stream.stop_stream() stream.close() p.terminate()Once we execute the above code, we can hear a wave. Note that we are not saving this wave in a
.wavfile.You may read here to learn about saving in a
.wavfile.
