Adjacency Matrix in Python

Aditya Raj Oct 10, 2023

Python Python Matrix

Create an Adjacency Matrix
Create an Adjacency Matrix in Python Using 2D Lists
Create an Adjacency Matrix in Python Using the NumPy Module
Conclusion

A graph data structure is used in Python to represent various real-life objects like networks and maps. We can represent a graph using an adjacency matrix.

This article will discuss different ways to implement the adjacency matrix in Python.

Create an Adjacency Matrix

Consider the following graph.

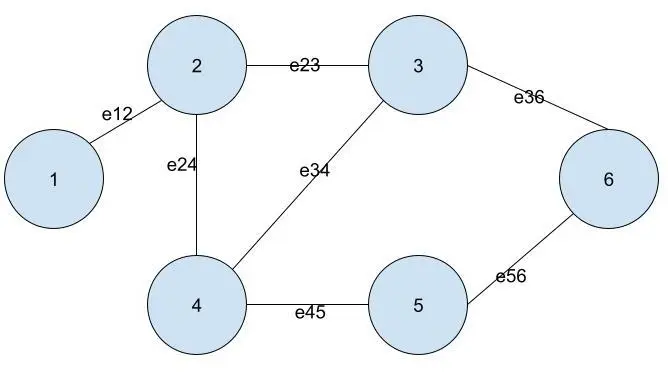
Python Adjacency Matrix Undirected Unweighted Graph

In the graph, there are 6 nodes numbered from 1 to 6. There are 7 edges in the graph connecting the nodes; an edge e_ij connects node i and node j.

To represent the graph, we use an adjacency matrix.

An adjacency matrix consists of a two-dimensional grid.
Each row or column in the grid represents a node.
For an unweighted graph, as shown above, if the value at the position (i,j) is 1 in the grid, it means that node i and node j are connected.
If the value at position (i,j) is 0, node i and node j are not connected.

If you want to create an adjacency matrix for the graph in the image above, it will look as follows.

| 0    | 1    | 0    | 0    | 0    | 0    |
| 1    | 0    | 1    | 1    | 0    | 0    |
| 0    | 1    | 0    | 1    | 0    | 1    |
| 0    | 1    | 1    | 0    | 1    | 0    |
| 0    | 0    | 0    | 1    | 0    | 1    |
| 0    | 0    | 1    | 0    | 1    | 0    |

The above table shows that the value at position (i,j) is also present at position (j,i). This is due to the reason that the edge e_ij is the same as the edge e_ji.

This also results in an adjacency matrix that is symmetrical along its diagonal.

In an unweighted graph, the edges have no weight. In other words, all the edges have equal weights.

Due to this, the adjacency matrix contains only the values 0 and 1.

Now, consider the following weighted graph.

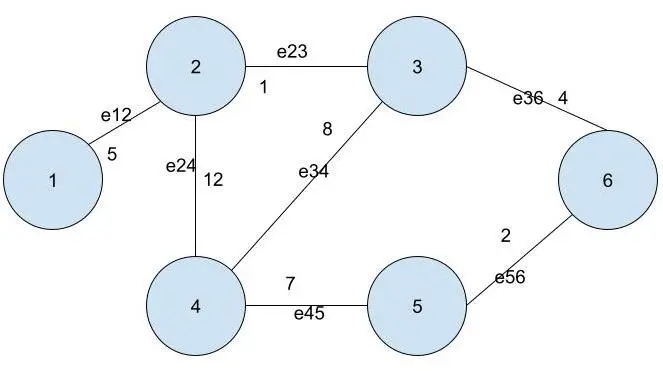
Python Adjacency Matrix Weighted Graph

For a weighted graph, everything remains the same except for the weights for the edges. You can observe that each edge has been assigned a value in the image.

Therefore, in the adjacency matrix, the value at position (i,j) is the weight of the edge e_ij in the graph.

The adjacency matrix for the above image looks as follows.

| 0    | 5    | 0    | 0    | 0    | 0    |
| 5    | 0    | 1    | 12   | 0    | 0    |
| 0    | 1    | 0    | 8    | 0    | 4    |
| 0    | 12   | 8    | 0    | 7    | 0    |
| 0    | 0    | 0    | 7    | 0    | 2    |
| 0    | 0    | 4    | 0    | 2    | 0    |

Again, you can observe that the value at position (i,j) in the matrix is also present at position (j,i). This is due to the reason that the edge e_ij is the same as the edge e_ji.

Again, this results in a symmetrical adjacency matrix along its diagonal.

Create an Adjacency Matrix in Python Using 2D Lists

To create an adjacency matrix for an unweighted graph with n nodes, we will first create a two-dimensional list containing n inner lists. Additionally, each inner list contains n zeros.

After creating a 2-dimensional list containing zeros, we will assign 1 to the positions (i,j) where the edge e_ij exists in the graph. For this task, we will use the following steps.

First, we will create an empty list named adjacency_matrix. After that, we will convert it into a 2-dimensional list using a for loop and the append() method.
Inside the for loop, we will create an empty list named row. Then, we will populate the empty list with zeros using another for loop, and finally, we will append row into the adjacency_matrix.
In the code, we have represented the set of edges using a list of tuples. Each tuple contains 2 values that represent the connected nodes of the graph.
After defining the edges, we will assign the value 1 to the positions where edges are present in the graph using a for loop.

Code:

import pprint

row_num = 6
col_num = 6
adjacency_matrix = []
for i in range(row_num):
    row = []
    for j in range(col_num):
        row.append(0)
    adjacency_matrix.append(row)
edges = [(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
for edge in edges:
    row = edge[0]
    col = edge[1]
    adjacency_matrix[row - 1][col - 1] = 1
    adjacency_matrix[col - 1][row - 1] = 1

print("The edges in the graph are:")
print(edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

Output:

The edges in the graph are:
[(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
The adjacency matrix is:
[[0, 1, 0, 0, 0, 0],
 [1, 0, 1, 1, 0, 0],
 [0, 1, 0, 1, 0, 1],
 [0, 1, 1, 0, 1, 0],
 [0, 0, 0, 1, 0, 1],
 [0, 0, 1, 0, 1, 0]]

In the code, you can observe that we have 0-based indexing. Due to this, each node (i,j) is represented by the position (i-1,j-1) in the adjacency matrix.

To create an adjacency matrix for a weighted graph, we will first create an n x n 2-dimensional list having 0s. After that, we will assign the weight of edge e_ij at the position (i,j) in the matrix.

You can observe this in the following example.

import pprint

row_num = 6
col_num = 6
adjacency_matrix = []
for i in range(row_num):
    row = []
    for j in range(col_num):
        row.append(0)
    adjacency_matrix.append(row)
weighted_edges = [
    (1, 2, 5),
    (2, 4, 12),
    (2, 3, 1),
    (3, 4, 8),
    (4, 5, 7),
    (3, 6, 4),
    (5, 6, 2),
]
for edge in weighted_edges:
    row = edge[0]
    col = edge[1]
    weight = edge[2]
    adjacency_matrix[row - 1][col - 1] = weight
    adjacency_matrix[col - 1][row - 1] = weight

print("The edges in the graph are:")
print(weighted_edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

Output:

The edges in the graph are:
[(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
The adjacency matrix is:
[[0, 5, 0, 0, 0, 0],
 [5, 0, 1, 12, 0, 0],
 [0, 1, 0, 8, 0, 4],
 [0, 12, 8, 0, 7, 0],
 [0, 0, 0, 7, 0, 2],
 [0, 0, 4, 0, 2, 0]]

In the above code, the edges have been represented using a triplet of numbers. The first 2 numbers represent the nodes of the graph that are connected by the edge.

The third number represents the weight of the edge.

Create an Adjacency Matrix in Python Using the NumPy Module

To make an adjacency matrix for a graph using the NumPy module, we can use the np.zeros() method.

The np.zeros() method takes a tuple in the form of (row_num,col_num) as its input argument and returns a two-dimensional matrix of shape row_num x col_num. Here, row_num and col_num are the number of rows and columns in the matrix.

We will use the following steps to create an adjacency matrix using the np.zeros() method.

First, we will create a size n x n matrix by passing a tuple (n,n) to the zeros() method.
Then, we will update the values to 1 at the position (i-1,j-1) for every edge e_ij in the graph; here, we use 0-based indexing. Due to this, the node (i,j) is represented by the position (i-1,j-1) in the code.

After executing the above steps, we will get the adjacency matrix, as shown in the following example.

import pprint
import numpy as np

row_num = 6
col_num = 6
adjacency_matrix = np.zeros((row_num, col_num), dtype=int)
edges = [(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
for edge in edges:
    row = edge[0]
    col = edge[1]
    adjacency_matrix[row - 1][col - 1] = 1
    adjacency_matrix[col - 1][row - 1] = 1

print("The edges in the graph are:")
print(edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

Output:

The edges in the graph are:
[(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
The adjacency matrix is:
array([[0, 1, 0, 0, 0, 0],
       [1, 0, 1, 1, 0, 0],
       [0, 1, 0, 1, 0, 1],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 0, 1],
       [0, 0, 1, 0, 1, 0]])

To create the adjacency matrix for the weighted graphs, we will update the values at the position (i,j) to the weight of the edge e_ij as shown below.

import pprint
import numpy as np

row_num = 6
col_num = 6
adjacency_matrix = np.zeros((row_num, col_num), dtype=int)
weighted_edges = [
    (1, 2, 5),
    (2, 4, 12),
    (2, 3, 1),
    (3, 4, 8),
    (4, 5, 7),
    (3, 6, 4),
    (5, 6, 2),
]
for edge in weighted_edges:
    row = edge[0]
    col = edge[1]
    weight = edge[2]
    adjacency_matrix[row - 1][col - 1] = weight
    adjacency_matrix[col - 1][row - 1] = weight

print("The edges in the graph are:")
print(weighted_edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

Output:

The edges in the graph are:
[(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
The adjacency matrix is:
array([[ 0,  5,  0,  0,  0,  0],
       [ 5,  0,  1, 12,  0,  0],
       [ 0,  1,  0,  8,  0,  4],
       [ 0, 12,  8,  0,  7,  0],
       [ 0,  0,  0,  7,  0,  2],
       [ 0,  0,  4,  0,  2,  0]])

Conclusion

This article discusses two ways to implement an adjacency matrix in Python. We suggest you implement an adjacency matrix with the NumPy module as it is much more efficient in terms of storage requirements.

Also, performing different operations on a NumPy array is much more efficient regarding time and memory requirements.

Author: Aditya Raj

Aditya Raj is a highly skilled technical professional with a background in IT and business, holding an Integrated B.Tech (IT) and MBA (IT) from the Indian Institute of Information Technology Allahabad. With a solid foundation in data analytics, programming languages (C, Java, Python), and software environments, Aditya has excelled in various roles. He has significant experience as a Technical Content Writer for Python on multiple platforms and has interned in data analytics at Apollo Clinics. His projects demonstrate a keen interest in cutting-edge technology and problem-solving, showcasing his proficiency in areas like data mining and software development. Aditya's achievements include securing a top position in a project demonstration competition and gaining certifications in Python, SQL, and digital marketing fundamentals.

GitHub

Adjacency Matrix in Python

Create an Adjacency Matrix

Create an Adjacency Matrix in Python Using 2D Lists

First, we will create an empty list named `adjacency_matrix`. After that, we will convert it into a 2-dimensional list using a `for` loop and the `append()` method.

Inside the `for` loop, we will create an empty list named `row`. Then, we will populate the empty list with zeros using another `for` loop, and finally, we will append `row` into the `adjacency_matrix`.

In the code, we have represented the set of edges using a list of tuples. Each tuple contains 2 values that represent the connected nodes of the graph.

After defining the edges, we will assign the value 1 to the positions where edges are present in the graph using a `for` loop.

Create an Adjacency Matrix in Python Using the NumPy Module

First, we will create a size `n x n` matrix by passing a tuple `(n,n)` to the `zeros()` method.

Then, we will update the values to 1 at the position `(i-1,j-1)` for every edge e_ij in the graph; here, we use 0-based indexing. Due to this, the node `(i,j)` is represented by the position `(i-1,j-1)` in the code.

Conclusion

Related Article - Python Matrix

Create an Adjacency Matrix

Create an Adjacency Matrix in Python Using 2D Lists

First, we will create an empty list named adjacency_matrix. After that, we will convert it into a 2-dimensional list using a for loop and the append() method.

Inside the for loop, we will create an empty list named row. Then, we will populate the empty list with zeros using another for loop, and finally, we will append row into the adjacency_matrix.

In the code, we have represented the set of edges using a list of tuples. Each tuple contains 2 values that represent the connected nodes of the graph.

After defining the edges, we will assign the value 1 to the positions where edges are present in the graph using a for loop.

Create an Adjacency Matrix in Python Using the NumPy Module

First, we will create a size n x n matrix by passing a tuple (n,n) to the zeros() method.

Then, we will update the values to 1 at the position (i-1,j-1) for every edge eij in the graph; here, we use 0-based indexing. Due to this, the node (i,j) is represented by the position (i-1,j-1) in the code.

Conclusion

Related Article - Python Matrix

First, we will create an empty list named `adjacency_matrix`. After that, we will convert it into a 2-dimensional list using a `for` loop and the `append()` method.

Inside the `for` loop, we will create an empty list named `row`. Then, we will populate the empty list with zeros using another `for` loop, and finally, we will append `row` into the `adjacency_matrix`.

After defining the edges, we will assign the value 1 to the positions where edges are present in the graph using a `for` loop.

First, we will create a size `n x n` matrix by passing a tuple `(n,n)` to the `zeros()` method.

Then, we will update the values to 1 at the position `(i-1,j-1)` for every edge e_ij in the graph; here, we use 0-based indexing. Due to this, the node `(i,j)` is represented by the position `(i-1,j-1)` in the code.