How to Plot NumPy Linear Fit in Matplotlib Python

This tutorial explains how to fit a curve to the given data using the numpy.polyfit() method and display the curve using the Matplotlib package.

import numpy as np
import matplotlib.pyplot as plt

x = [1, 2, 3, 1.5, 4, 2.5, 6, 4, 3, 5.5, 5, 2]
y = [3, 4, 8, 4.5, 10, 5, 15, 9, 5, 16, 13, 3]

plt.scatter(x, y)
plt.title("Scatter Plot of the data")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

Output:

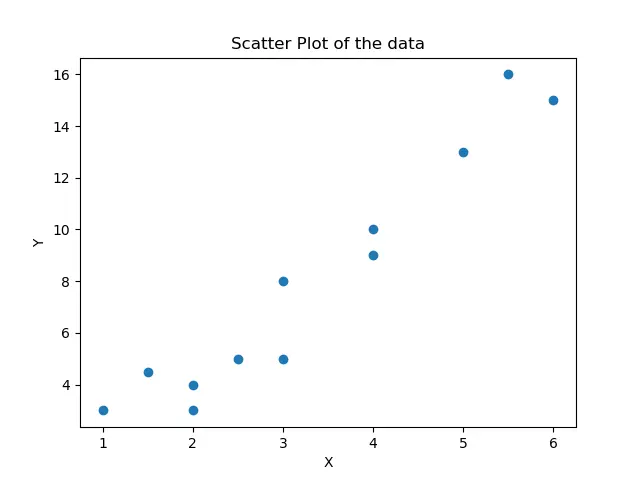
It displays the scatter plot of data on which curve fitting needs to be done. We can see that there is no perfect linear relationship between the X and Y values, but we will try to make the best linear approximate from the data.

Plot the linear fit to the data

import numpy as np
import matplotlib.pyplot as plt

x = [1, 2, 3, 1.5, 4, 2.5, 6, 4, 3, 5.5, 5, 2]
y = [3, 4, 8, 4.5, 10, 5, 15, 9, 5, 16, 13, 3]

plt.scatter(x, y, color="red")
plt.title("Scatter Plot of the data")
plt.xlabel("X")
plt.ylabel("Y")

linear_model = np.polyfit(x, y, 1)
linear_model_fn = np.poly1d(linear_model)
x_s = np.arange(0, 7)
plt.plot(x_s, linear_model_fn(x_s), color="green")

plt.show()

Output:

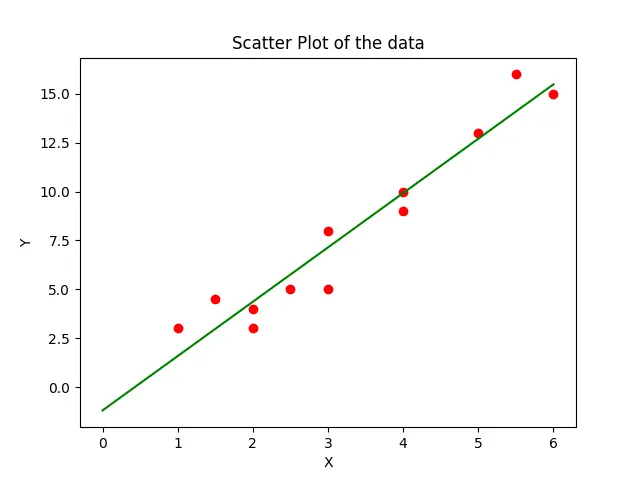
Here, we try to approximate the given data by the equation of the form y=m*x+c. The polyfit() method will estimate the m and c parameters from the data, and the poly1d() method will make an equation from these coefficients. We then plot the equation in the figure using the plot() method represented by the green color’s straight line.

In the example, we fit a linear equation to the data as we have 1 as the third argument in the polyfit() method. We can also experiment with other values of the parameter to fit higher order curves to the data.

import numpy as np
import matplotlib.pyplot as plt

x = [1, 2, 3, 1.5, 4, 2.5, 6, 4, 3, 5.5, 5, 2]
y = [3, 4, 8, 4.5, 10, 5, 15, 9, 5, 16, 13, 3]

plt.scatter(x, y, color="red")
plt.title("Scatter Plot of the data")
plt.xlabel("X")
plt.ylabel("Y")

linear_model = np.polyfit(x, y, 2)
linear_model_fn = np.poly1d(linear_model)
x_s = np.arange(0, 7)
plt.plot(x_s, linear_model_fn(x_s), color="green")

plt.show()

Output:

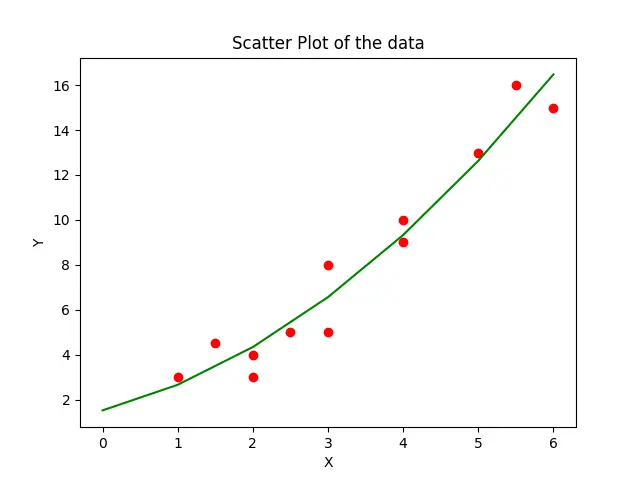
In this way, we can generate a quadratic plot to the data by simply setting the third parameter of the polyfit() method to 2 which fits the second-order curve to the data.