Recursive Fibonacci in C++

1. Recursive Functions in C++
2. Types of Recursion
3. Fibonacci Series
4. Fibonacci Series in C++

This small tutorial will explain how to implement the Fibonacci series using the recursive function in C++. For that, we will have a brief intro about recursive functions first.

Recursive Functions in C++

A recursive function invokes itself within its own body, and using this concept is called recursion. This concept is useful in many ways, and some functions can be implemented using recursion only.

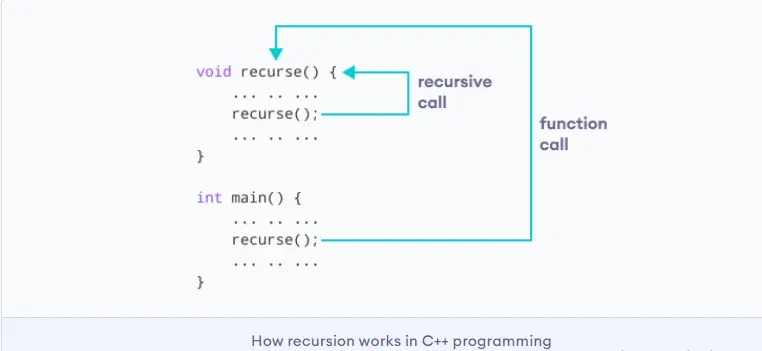
The figure above shows the concept of recursion. In the main function, a function recurse is called, and in that function, recurse is called again.

This will create a recursive call, and the program will continue its iterations in this function until some condition is met. Usually, the if...else structure is used in the recursive functions, with one path making a recursive call and the other exiting from the function; Otherwise, infinite recursion will occur.

Recursion makes several repeated calls to the function from within the function. The recursive condition invokes the function again until the base case is satisfied.

The base case is contained inside the function, and it terminates the execution whenever the condition of the base case is met.

Code:

void recursiveFun(int x) {
  if (x == 0) return;
  x = x - 1;
  recursiveFun(x);
}

The above function, once called with argument x, will recursively call itself with a reduced value of x (i.e., [x-1, x-2,…, x-(x-1)]) until the x becomes zero. When x with value zero is encountered, the program stops generating new recursive calls and starts returning values (if any) from bottom to top.

Although the recursion can be used to solve almost all the problems, there are selective instances where it is truly beneficial. It is commonly used to handle difficult issues and problems that follow a hierarchical pattern; it addresses the main problem by resolving smaller subproblems.

Types of Recursion

Direct Recursion and Indirect Recursion are the two types of recursion.

Direct Recursion

The recursive function calls itself directly in its own body through direct recursion.

void recursion() { ....recursion(); }

In the code, we can see that the function is calling itself in its own body or parenthesis.

Indirect Recursion

In indirect recursion, the function is called indirectly in any other function’s body.

void func1() { ... func2(); }
void func2() { ... func1(); }

Fibonacci Series

The Fibonacci series is a set of integers in which each successive number is the sum of the two preceding ones. The first two numbers, 0 and 1, and the third are calculated by adding the first two together.

The formula to calculate the Fibonacci series is:

For example 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

We can see that the third element, 1, is the sum of 0+1. Similarly, the fourth number, 2, is the sum of the previous numbers (1+1=2).

Hence we can predict the next element of the series to be 21+34 = 55.

Fibonacci Series in C++

To implement the Fibonacci series, we can implement a recursive function that can take the input a number and will print the Fibonacci series of that quantity. For example, if the user enters 8, we will print 8 numbers of the series.

Code:

#include <iostream>
using namespace std;

int fibonacci(int num) {
  if (num <= 1) return num;
  return fibonacci(num - 1) + fibonacci(num - 2);
}

int main() {
  int num;
  cout << "Enter a number: ";
  cin >> num;
  for (int a = 0; a < num; a++) {
    cout << fibonacci(a) << " ";
  }
  return 0;
}

In the main function, we have prompt the user to enter a number. After that, we have iterated a loop from 0 to that input number num and passed the iterator variable a to the Fibonacci function.

This loop will iterate num times the number entered by the user. In the function Fibonacci, we have an if condition that will check if the number is less than 1, then it will return that number.

Otherwise, it will call the fibonacci function for num-1 and num-2 because every next number of the series is calculated by making a sum of the previous two numbers, i.e., n-1 and n-2.

Output:

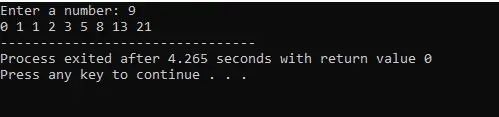
The user has entered the number 9, so the Fibonacci series has been printed having 9 values in it.