How to Read File Into a Binary Search Tree Using C++
- Binary Search Tree in C++
- Insertion in Binary Search Tree in C++
- Deletion in Binary Search Tree in C++
- Read the File Into a Binary Search Tree in C++
This tutorial will discuss reading the file into a binary search tree in C++. First, we will quickly discuss the binary search tree and its operation.
Later we will see how to read the file into a binary search tree.
Binary Search Tree in C++
The binary search tree is a binary tree with a special arrangement of nodes, which later helps in the search. It is worth mentioning here that statistics show that more than 90% of operations are search operations, whereas; less than 10% of operations include insert, update, delete, etc.
In the binary search tree, each node is placed such that the node is always larger than its left child and smaller than equal (in case of duplication) to its right child.
This definition recursively applies to every node of the tree. Thus, we always have a root larger than all nodes in its left sub-tree and smaller than equal to all nodes in its right sub-tree.
5 / 3 8 / \ / 1 2 6 9
Here, you can see an example of a binary search tree, which is self-explanatory; as earlier, a binary search tree helps in the search operation.
For example, if we want to search 7 (say it key) in the above tree. We will compare the key with root node 5.
The key is larger than the root element; therefore, we have to search for the key in the right sub-tree only because all values on the left sub-tree are smaller than the root node.
Next, we will compare the key with 8 and move towards the left sub-tree of 8 because the key is smaller than 8. Next, we will compare 6 with the key and move towards the right sub-tree of 6.
In the right of 6, we have NULL; therefore, we will stop the element not found. We did 3 comparisons instead of 6.
The more elements we have in the tree, the ratio of comparisons with total elements in the tree will further reduce. The search seems trivial; however, we will give you the complete code later.
Before presenting the complete code, let’s discuss insertion and deletion operations in the BST. However, it’s better first to see the definition of class Node.
template <class T>
class Node {
public:
T data;
Node* left;
Node* right;
Node(T data) {
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
Here, we have used a template to use the same tree for any data type. We will show you its benefit when we will use our BST.
In our definition of the Node class, we have data of the template type, which we can select at the time of object creation. We have left and right pointers as we will implement our trees linked implementation.
In the constructor, besides data, we assign NULL to the left and right pointers because every new node in the start has no left and right child nodes.
Insertion in Binary Search Tree in C++
Consider insertion of the new element in the BST. There are two possible cases either the tree is empty or has one or more nodes.
The first case is the tree is empty; the new element will become the tree’s root node after this insertion. In the second case, the new node will become either left or right child of some existing node.
Therefore, we will start from the root node, comparing the node’s value with our new value; we will move either on the left of the current node or on the right of the current node.
Finally, we will reach a point where we have NULL (no node); we will create a new node and make it a left or right child according to the node’s and the new node’s values.
For example, if we insert node 7 in the BST, the new BST will be:
5 / 2 8 / \ /
1 3 6 9
7
Starting from the root node, 5 is smaller than 7, so move to the right. 8 is larger, so we move to the left side. 6 is smaller; therefore, move to the right.
On the right, there is no node, so we create a new node and make it the right child of node 6. We will see the implementation of the insertion function, but before that, see the definition of class BST.
template <class T>
class BST {
Node<T> *root;
public:
BST() { root = NULL; }
...
Once again, we have created a template class for BST, with only the data member root of type Node<T>. In the constructor, we have assigned NULL to the root node, which means the tree is empty.
Therefore, in case of deletion, whenever we will delete the last node, we will assign NULL to the root node. Let’s see the insert function.
Node<T>* insert(T key) { root = insert(root, key); }
Node<T>* insert(Node<T>* temp, T key) {
if (temp == NULL) return new Node<T>(key);
if (temp->data > key)
temp->left = insert(temp->left, key);
else
temp->right = insert(temp->right, key);
return temp;
}
First, we have a wrapper function to call the workhorse function, which performs the insertion task. The reason for writing the wrapper function is that, for security reasons, we don’t want to give access to the root node outside the class.
Click the wrapper function if you want to know about wrapper functions.
In our workhorse function, we have a recursive implementation, where the base case is a NULL node, where we will create a new node and return its address to the caller, which will assign this address to either left or right child to link the new node in the tree.
If we don’t have a NULL node, we will compare the data and move to the right or left depending on whether the current node has a smaller or larger value, as we already discussed the search strategy.
Deletion in Binary Search Tree in C++
Like insertion, there are two possible cases in the deletion of an element in the BST. Either we are deleting the last node, the root node, or we are deleting some node where we have more than one node in the tree, such that the tree will not become empty after the deletion of the current node.
In the first case, we delete the node and assign NULL to the root node. In the second case, we have three possibilities:
- node has no child node
- node has only one child node
- node has both left and right child nodes
The first two schemes are very simple. In case there is no child node.
Delete node and return NULL (as we have recursive definition again) so that in calling function, the parent node will assign NULL to its right or left pointer.
If the node has one child node, replace the child node with the current node and delete the current node. As a result, the child node will be assigned to the grandfather instead of the father because the father will die (sorry for this analogy).
The last case is tricky, where a node has both left and right children. In this case, we have two choices.
First, select the left-most descendent node from the current node’s right sub-tree or the right-most descendent node from the left sub-tree. In both cases, copy the value of the select node at the current node.
Now, we have two nodes in the BST with the same value; therefore, we will again call the recursive delete function at the left sub-tree or right sub-tree of the current node.
Consider the example; suppose we want to delete 5 from the root node. We can select node 6 from the right sub-tree, being left most node in the right sub-tree of 5, or we can select node 3 from the left sub-tree, which is the right-most node in the left sub-tree of 5.
5 3 6 / \ / \ / 2 8 2 8 2 8 / \ / \ / / \ / \ 1 3 6 9 1 6 9 1 3 9
Let’s see the implementation of the delete function.
Node<T>* deleteNode(T key) { root = deleteNode(root, key); }
Node<T>* deleteNode(Node<T>* temp, T key) {
if (temp == NULL) return temp;
if (temp->data > key)
temp->left = deleteNode(temp->left, key);
else if (temp->data < key)
temp->right = deleteNode(temp->right, key);
else {
if (temp->left == NULL && temp->right == NULL) {
delete temp;
temp = NULL;
} else if (temp->left == NULL) {
Node<T>* curr = temp;
temp = temp->right;
delete curr;
} else if (temp->right == NULL) {
Node<T>* curr = temp;
temp = temp->left;
delete curr;
} else {
Node<T>* toBeDeleted = findMinNode(temp->right);
temp->data = toBeDeleted->data;
temp->right = deleteNode(temp->right, toBeDeleted->data);
}
}
return temp;
}
Again, first, we have a wrapper function. Next, we have the workhorse function.
In the first three lines, we are searching for our target node. The target value doesn’t exist in the tree in this case; ultimately, we will reach the NULL node.
Otherwise, there are three cases, either the current node is larger than the key or smaller than the key, or the current node is our target node (in which case, we will move to the other part).
In the other part, we are handing three cases; we already discussed that is target node has no child node, only the right child node, only the left child node, and both the left and right child (handled in the other part).
In this part, we use the function findMinNode to select the smallest node from the right sub-tree of the current/target node. Now, see the entire class of BST.
#include <iostream>
using namespace std;
template <class T>
class Node {
public:
T data;
Node* left;
Node* right;
Node(T data) {
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
template <class T>
class BST {
Node<T>* root;
public:
BST() { root = NULL; }
Node<T>* insert(T key) { root = insert(root, key); }
Node<T>* insert(Node<T>* temp, T key) {
if (temp == NULL) return new Node<T>(key);
if (temp->data > key)
temp->left = insert(temp->left, key);
else
temp->right = insert(temp->right, key);
return temp;
}
Node<T>* findMinNode(Node<T>* temp) {
while (temp->left != NULL) temp = temp->left;
return temp;
}
Node<T>* deleteNode(T key) { root = deleteNode(root, key); }
Node<T>* deleteNode(Node<T>* temp, T key) {
if (temp == NULL) return temp;
if (temp->data > key)
temp->left = deleteNode(temp->left, key);
else if (temp->data < key)
temp->right = deleteNode(temp->right, key);
else {
if (temp->left == NULL && temp->right == NULL) {
delete temp;
temp = NULL;
} else if (temp->left == NULL) {
Node<T>* curr = temp;
temp = temp->right;
delete curr;
} else if (temp->right == NULL) {
Node<T>* curr = temp;
temp = temp->left;
delete curr;
} else {
Node<T>* toBeDeleted = findMinNode(temp->right);
temp->data = toBeDeleted->data;
temp->right = deleteNode(temp->right, toBeDeleted->data);
}
}
return temp;
}
void preOrder() {
preOrder(root);
cout << '\n';
}
void preOrder(Node<T>* temp) {
if (temp == NULL) return;
cout << temp->data << " ";
preOrder(temp->left);
preOrder(temp->right);
}
void inOrder() {
inOrder(root);
cout << '\n';
}
void inOrder(Node<T>* temp) {
if (temp == NULL) return;
inOrder(temp->left);
cout << temp->data << " ";
inOrder(temp->right);
}
};
int main() {
BST<int> tree;
tree.insert(40);
tree.insert(22);
tree.insert(15);
tree.insert(67);
tree.insert(34);
tree.insert(90);
tree.preOrder();
tree.inOrder();
tree.deleteNode(40);
cout << "After deleting 40 temp from the tree\n";
tree.preOrder();
tree.inOrder();
return 0;
}
We have the entire BST class with inOrder and preOrder traversal functions to see the shape of our tree. We can build our BST from in-order and preorder traversal or in-order and post-order traversal; you may read this article.
Let’s see the output of the code.
40 22 15 34 67 90
15 22 34 40 67 90
After deleting 40 temp from the tree
67 22 15 34 90
15 22 34 67 90
In this output, the first line has preorder traversal, and the second line has in-order traversal. First of all, in-order BST always gives sorted elements.
Therefore, the second line somehow confirms that our code is doing insertion properly.
We can construct a binary tree from the first two lines (traversals). Pre-order always starts traversal from the root node; therefore, 40 is the root node.
If we see 40 in in-order traversal (second line), we can partition our binary tree into left and right sub-trees, where 67 and 90 are in the right sub-tree, and 15, 22, and 34 are in left-sub-tree; similarly, we can complete the remaining binary tree. Finally, our binary tree is:
40 / 22 67 / \ 15 34 90
This binary tree has properties of BST and shows that our code is working fine; similarly, we can construct a binary tree after deleting 40.
67 / 22 90 / 15 34
Node 40 is our target node, having both left & right child nodes. We have selected the left most from the right sub-tree, which is 67 because 67 has no left child; therefore, we have copied the value 67 at our target node and called the delete function again to delete 67 from the right sub-tree of the root.
Now, we have a case where 67 has the only right child, 90; therefore, we will replace 90 with 67. As a result, 90 will become the right child of 67.
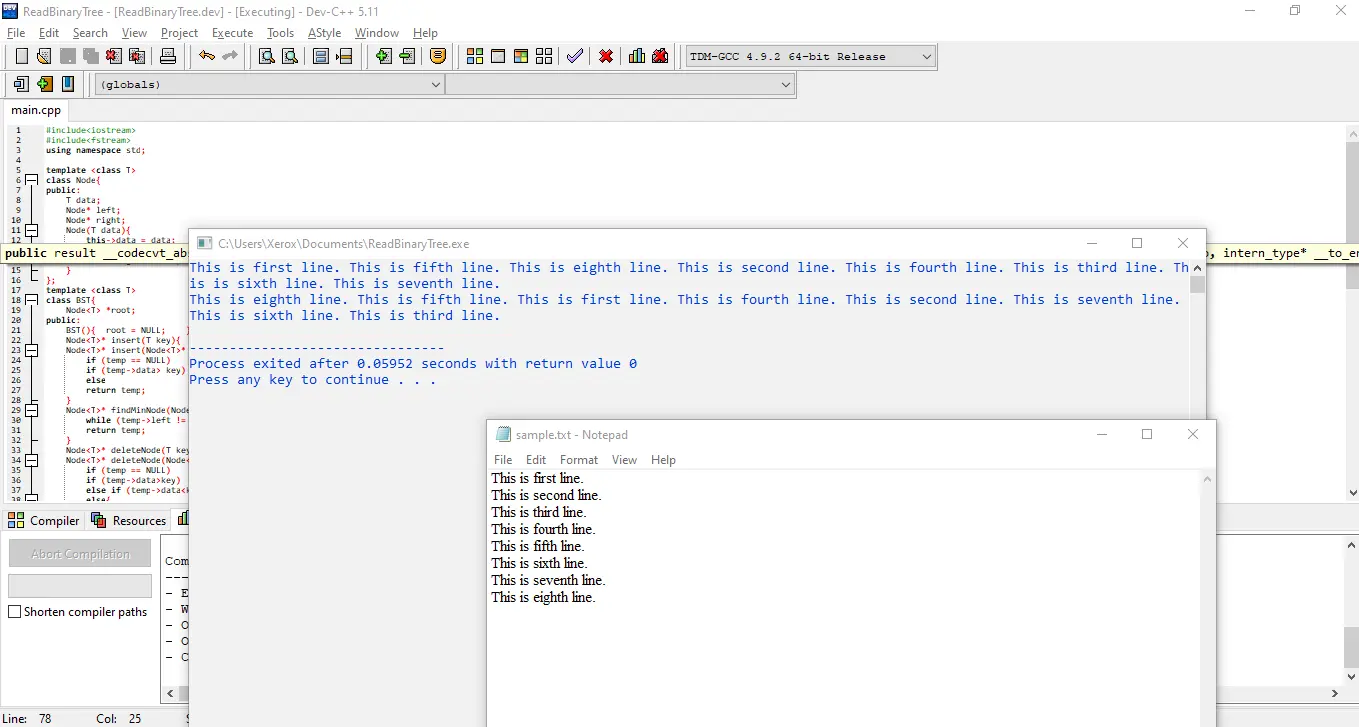
Read the File Into a Binary Search Tree in C++
Finally, now we can discuss the reading of files into BST. Again, we will do it step by step.
First, consider the following file.
This is first line.
This is second line.
This is third line.
This is fourth line.
This is fifth line.
This is sixth line.
This is seventh line.
This is eighth line.
We can read this file easily in C++ using the getline function. See the code:
#include <fstream>
#include <iostream>
using namespace std;
int main() {
ifstream in("sample.txt");
string s;
while (getline(in, s)) cout << s << '\n';
in.close();
}
We will have the same output as you can see in the file’s contents in the previous box. However, our objective is to place text in BST so that we can do a faster search.
So, it’s simple; we have already implemented BST in the class template, which we can use for strings as well; all we have to do is to create an object of BST accordingly.
You can save contents in the file sample.txt to read the file through code. Here, we have the code to read the file into a binary search tree.
#include <fstream>
#include <iostream>
using namespace std;
template <class T>
class Node {
public:
T data;
Node* left;
Node* right;
Node(T data) {
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
template <class T>
class BST {
Node<T>* root;
public:
BST() { root = NULL; }
Node<T>* insert(T key) { root = insert(root, key); }
Node<T>* insert(Node<T>* temp, T key) {
if (temp == NULL) return new Node<T>(key);
if (temp->data > key)
temp->left = insert(temp->left, key);
else
temp->right = insert(temp->right, key);
return temp;
}
Node<T>* findMinNode(Node<T>* temp) {
while (temp->left != NULL) temp = temp->left;
return temp;
}
Node<T>* deleteNode(T key) { root = deleteNode(root, key); }
Node<T>* deleteNode(Node<T>* temp, T key) {
if (temp == NULL) return temp;
if (temp->data > key)
temp->left = deleteNode(temp->left, key);
else if (temp->data < key)
temp->right = deleteNode(temp->right, key);
else {
if (temp->left == NULL && temp->right == NULL) {
delete temp;
temp = NULL;
} else if (temp->left == NULL) {
Node<T>* curr = temp;
temp = temp->right;
delete curr;
} else if (temp->right == NULL) {
Node<T>* curr = temp;
temp = temp->left;
delete curr;
} else {
Node<T>* toBeDeleted = findMinNode(temp->right);
temp->data = toBeDeleted->data;
temp->right = deleteNode(temp->right, toBeDeleted->data);
}
}
return temp;
}
void preOrder() {
preOrder(root);
cout << '\n';
}
void preOrder(Node<T>* temp) {
if (temp == NULL) return;
cout << temp->data << " ";
preOrder(temp->left);
preOrder(temp->right);
}
void inOrder() {
inOrder(root);
cout << '\n';
}
void inOrder(Node<T>* temp) {
if (temp == NULL) return;
inOrder(temp->left);
cout << temp->data << " ";
inOrder(temp->right);
}
};
int main() {
BST<string> tree;
ifstream in("sample.txt");
string s;
while (getline(in, s)) tree.insert(s);
tree.preOrder();
tree.inOrder();
in.close();
return 0;
}
Output:

Again, first, we have preorder traversal, which shows the root node is This is the first line; however if we see in-order traversal, we have output in sorted order.
That is, eighth starting from e, the smallest letter among first, second, third, fourth, fifth, sixth, seventh, and eighth, whereas next, we have fifth, which is smaller than first because f in fifth is smaller than r in first.