2D Interpolation in Python

1. Use scipy.interpolate.interp2d to Create 2D Interpolation in Python
2. Use scipy.interpolate.Rbf to Create Radial Basis Function for Interpolation in Python

This article shows how to do interpolation in Python and looks at different 2d implementation methods. We will discuss useful functions for bivariate interpolation such as scipy.interpolate.interp2d, numpy.meshgrid, and Radial Basis Function for smoothing/interpolation (RBF) used in Python.

We will implement interpolation using the SciPy and Numpy libraries, making it easy.

Use scipy.interpolate.interp2d to Create 2D Interpolation in Python

First of all, let’s understand interpolation, a technique of constructing data points between given data points. Let’s assume two points, such as 1 and 2.

In this example, we can interpolate and find points 1.22 and 1.44, and many more.

Interpolation is often used in Machine Learning to fill in missing data in a dataset, called imputation. Interpolation is frequently used to make a dataset’s points more uniform.

Let’s see working with examples of interpolation in Python using the scipy.interpolate module.

The interp2d is a straightforward generalization of the interp1d function. This function takes the x and y coordinates of the available data points as separate one-dimensional arrays and a two-dimensional array of values for each pair of x and y coordinates.

The data points are assumed to be on a regular and uniform x and y coordinate grid. The general function form is below.

class scipy.interpolate.interp2d(x, y, z, kind='linear', copy=True, bounds_error=False, fill_value=None)

Where x, y, and z are arrays, the kind could be {'linear', 'cubic', 'quintic'} or may be left as optional. See also scipy.interpolate.interp2d detailed documentation.

# import libraries
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

# x,y arrays
x = np.arange(-5.01, 5.01, 0.25)
y = np.arange(-5.01, 5.01, 0.25)
xx, yy = np.meshgrid(x, y)  # see details below for 'np.meshgrid'

# approximate function which is z:= f(x,y)
z = np.sin(xx ** 2 + yy ** 2)
fun = interpolate.interp2d(
    x, y, z, kind="linear"
)  # kind could be {'linear', 'cubic', 'quintic'}
xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 5.01, 1e-2)
znew = fun(xnew, ynew)

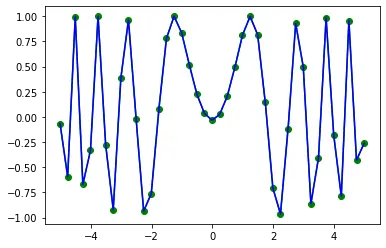
plt.plot(x, z[0, :], "go-", xnew, znew[0, :], "b-")
plt.show()

Output:

Note that we have used numpy.meshgrid to make the grid; you can make a rectangular grid out of two one-dimensional arrays representing Cartesian or Matrix indexing. See numpy.meshgrid documentation.

The general function form is below.

numpy.meshgrid(*xi, copy=True, sparse=False, indexing="xy")

The xi represents one-dimensional coordinate arrays x1, x2,…, xn.

Use scipy.interpolate.Rbf to Create Radial Basis Function for Interpolation in Python

This class of interpolation is used in the case of n-dimensional scattered data; for this, we use scipy.interpolate.Rbf.

import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate.rbf import Rbf  # radial basis functions

# x y arrays
x = [1, 1, 2, 3, 4, 4, 2, 6, 7]
y = [0, 2, 5, 6, 2, 4, 1, 5, 2]
z = [1] * len(x)

# RBF Func
rbf_fun = Rbf(x, y, z, function="gaussian")

x_new = np.linspace(0, 8, 81)
y_new = np.linspace(0, 8, 82)

x_grid, y_grid = np.meshgrid(x_new, y_new)
z_new = rbf_fun(x_grid.ravel(), y_grid.ravel()).reshape(x_grid.shape)

plt.pcolor(x_new, y_new, z_new)
plt.plot(x, y, "o")
plt.xlabel("x")
plt.ylabel("y")
plt.title("RBF Gaussian interpolation")

Output:

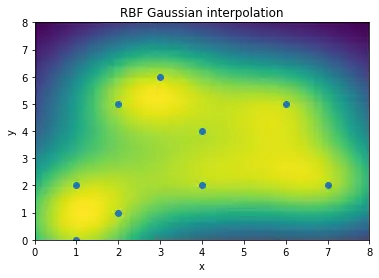
This class of interpolating functions converts N-D scattered data to M-D with radial basis functions (RBF). Smoothing and interpolating scattered data in n-dimensions can be accomplished using RBF interpolation.

Still, as there is a chance of extrapolation, like getting values outside the data range, this should be done carefully.