Tree Sort

1. Tree Sort Algorithm
2. Tree Sort Example
3. Tree Sort Algorithm Implementation
4. Tree Sort Algorithm Complexity

Tree sort is an online sorting algorithm. It uses the binary search tree data structure to store the elements. The elements can be retrieved in sorted order by doing an in-order traversal of the binary search tree. Since it is an online sorting algorithm, the elements inserted are always maintained in sorted order.

Tree Sort Algorithm

Let us assume that we have an unsorted array A[] containing n elements.

TreeSort()

Insert()

Inorder()

Tree Sort Example

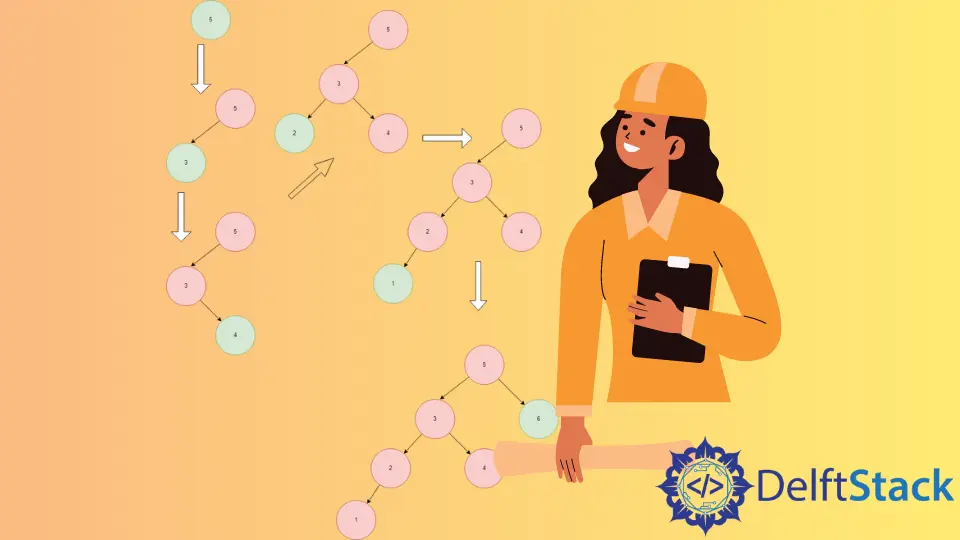
Suppose we have the array: (5, 3, 4, 2, 1, 6). We will sort it using the insertion sort algorithm.

First, we initialize BST by creating the root node 5.

3 is smaller than 5, so it gets inserted into the left of 5.

4 is smaller than 5 but large than 3, so it gets inserted into the right of 3 but left of 4.

2 is the smallest element in the current tree, so it gets inserted at the leftmost position.

1 is the smallest element in the current tree, so it gets inserted at the leftmost position.

6 is the largest element in the current tree, so it gets inserted at the rightmost position.

After the BST has been built, we perform in-order traversal on the tree to get the final sorted array (1, 2, 3 ,4, 5, 6).

Tree Sort Algorithm Implementation

#include <bits/stdc++.h>

using namespace std;

class Node {
 public:
  int key;
  Node *left, *right;
};

Node *newNode(int item) {
  Node *temp = new Node;
  temp->key = item;
  temp->left = temp->right = NULL;
  return temp;
}

void inorder(Node *root, int arr[], int &i) {
  if (root != NULL) {
    inorder(root->left, arr, i);
    arr[i++] = root->key;
    inorder(root->right, arr, i);
  }
}

Node *insertintoBST(Node *node, int key) {
  if (node == NULL) return newNode(key);
  if (key < node->key)
    node->left = insertintoBST(node->left, key);
  else if (key > node->key)
    node->right = insertintoBST(node->right, key);
  return node;
}

void treeSort(int arr[], int n) {
  Node *root = NULL;
  root = insertintoBST(root, arr[0]);
  for (int i = 1; i < n; i++) root = insertintoBST(root, arr[i]);
  int i = 0;
  inorder(root, arr, i);
}

int main() {
  int n = 6;
  int arr[6] = {5, 3, 4, 2, 1, 6};
  cout << "Input array: ";
  for (int i = 0; i < n; i++) {
    cout << arr[i] << " ";
  }
  cout << "\n";
  treeSort(arr, n);  // Sort elements in ascending order
  cout << "Output array: ";
  for (int i = 0; i < n; i++) {
    cout << arr[i] << " ";
  }
  cout << "\n";
}

Tree Sort Algorithm Complexity

Time Complexity

• Average Case

In average-case, the time complexity of inserting n nodes in a BST is of the order of O(nlogn). It occurs when the BST formed is a balanced BST. Hence the time complexity is of the order of [Big Theta]: O(nlogn).

• Worst Case

The worst-case occurs when the array is sorted, and an unbalanced binary search tree having a maximum height of O(n) is formed. It requires O(n) time for traversal and O(n²) for insertion as compared to the O(logn) time for traversal in case of a regular BST of height logn. The worst-case time complexity is [Big O]: O(n²).

It can be reduced to O(nlogn) using a self-balancing data structure like AVL tree, Red-Black Tree, etc.

• Best Case

The best-case occurs when the binary search tree formed is balanced. The best-case time complexity is [Big Omega]: O(nlogn). It is the same as average-case time complexity.

Space Complexity

Space Complexity for this algorithm is O(n) because n nodes have to be created for each element inside the binary search tree.