How to Implement a Tree Data Structure in Python

1. Implement a Tree Structure From Scratch in Python
2. Traverse a Binary Tree in Python
3. Implement a Tree Using a Python Library

A Tree is one of the data structures. A data structure is nothing but how we organize the data in memory. A Tree is a combination of nodes (also known as vertices) and edges. A tree can have any number of nodes and edges. A node is where we store the data, and an edge is a path between 2 nodes. There are various types of trees available like a binary tree, ternary tree, binary search tree, AVL tree, etc.

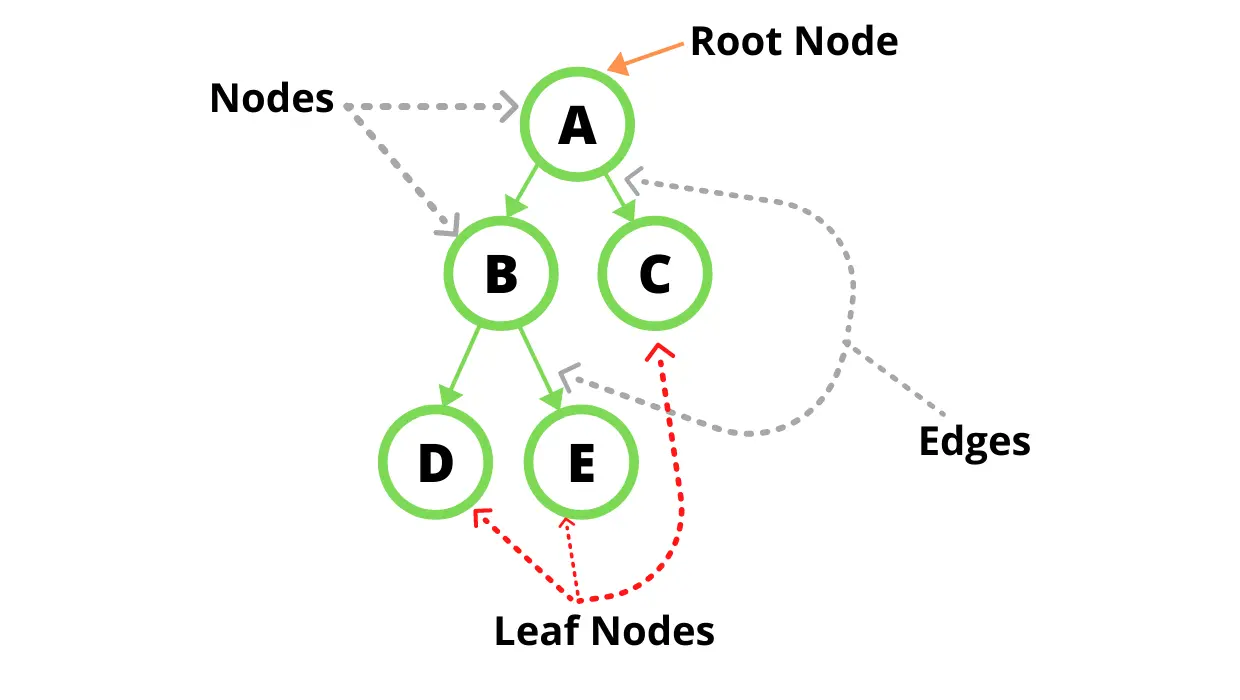
Types of nodes in a tree:

1. Parent Node: A node that has one or more children.
2. Child Node: A node that has a parent node.
3. Leaf Node: A node that doesn’t have any children.

In this article, let’s first see how to implement a tree from scratch without using any library, and later you will see how to implement a tree with the help of a Python library.

Implement a Tree Structure From Scratch in Python

To create a tree in Python, we first have to start by creating a Node class that will represent a single node. This Node class will contain 3 variables; the first is the left pointing to the left child, the second variable data containing the value for that node, and the right variable pointing to the right child.

class Node:
    def __init__(self, data):
        self.left = None
        self.right = None
        self.data = data

Let’s initialize a tree.

root = Node(10)

root.left = Node(34)
root.right = Node(89)
root.left.left = Node(45)
root.left.right = Node(50)

The tree looks like below.

          10
        /    \
       34      89
     /    \ 
    45    50 

Whenever you create an object of class Node, the __init__ constructor will be called, and all the variables inside that constructor will be initialized. The root contains the root node of the tree, which has a value of 10, and root.left and root.right using which we will insert the left child with the value 34 and the right child to the root node with the value 89. Since it is a binary tree, every node will contain at most two nodes.

In the end, we insert two more nodes to the tree i.e 45 and 50, as the children for the node 34. You can insert any number of nodes you want inside a tree depending upon the type of tree you are creating.

Traverse a Binary Tree in Python

Now we have created a tree, so let’s traverse the tree to print the tree elements. A traversing visits every node in a tree. Every node in a tree will be visited three times in the traversal. A way in which we traverse a tree is from top to bottom and left to right.

Pre-Order Traversal

While traversing a tree, whenever we see the node for the first time, we print that node, and then we perform recursion on the left node and then on the right node.

def preorder(node):
    if node:
        print(node.data)
        preorder(node.left)
        preorder(node.right)

Output:

10 
34 
45 
50 
89

In-Order Traversal

While performing in-order traversal, we first perform recursion on the left node, and then as we visit the same node for the second time, we print that node. Then we perform recursion on the right node.

def inorder(node):
    if node:
        inorder(node.left)
        print(node.data)
        inorder(node.right)

Output:

45 
34 
50 
10 
89

Post-Order Traversal

For Post-order traversal, we perform recursion on the left node and the right node, and then as we visit the same node for the third time, we print that node.

def postorder(node):
    if node:
        postorder(node.left)
        postorder(node.right)
        print(node.data)

Output:

45
50
34
89
10

Implement a Tree Using a Python Library

As we have seen, implementing a tree from scratch takes some time and needs a lot of code. An easier way to implement a tree in Python is by using a library called anytree. The anytree library allows you to create a tree without writing a ton of code.

To use the anytree library, we first have to install it with the below command’s help.

pip install anytree

Here, also we are creating the same tree which we have previously created. Now we can import Node and RenderTree from the anytree library.

from anytree import Node, RenderTree

root = Node(10)

level_1_child_1 = Node(34, parent=root)
level_1_child_2 = Node(89, parent=root)
level_2_child_1 = Node(45, parent=level_1_child_1)
level_2_child_2 = Node(50, parent=level_1_child_2)

for pre, fill, node in RenderTree(root):
    print("%s%s" % (pre, node.name))

# Tree Structure
#          10
#        /    \
#       34      89
#     /    \
#    45    50

Output:

10
├── 34
│   └── 45
└── 89
    └── 50

Here, the Node will create a node for us that takes two parameters; the first is the node’s value, and the second is the name of the parent node (this is an optional parameter). Since in our tree root node is the only node that does not have any parent, while creating the root node, we will only pass the first parameter: the node’s value and not the second parameter. The RenderTree method will help us to print the entire tree as shown in the output.