How to Implement Min Heap in Python

1. The Min Heap in Python
2. Create a Class to Implement Min Heap in Python
3. Use the heapq Module to Implement Min Heap in Python

Trees are a non-linear data structure where elements are arranged at multiple levels. Heap is a data structure based on trees.

It is a complete binary tree which means that every parent node has two children nodes. Heaps implement different algorithms, sort other structures, prioritize queues, etc.

Heaps are of two types - max and min. These are based on the value of the children node in comparison to the parent node.

This tutorial will discuss the Min Heap and its implementation in Python.

The Min Heap in Python

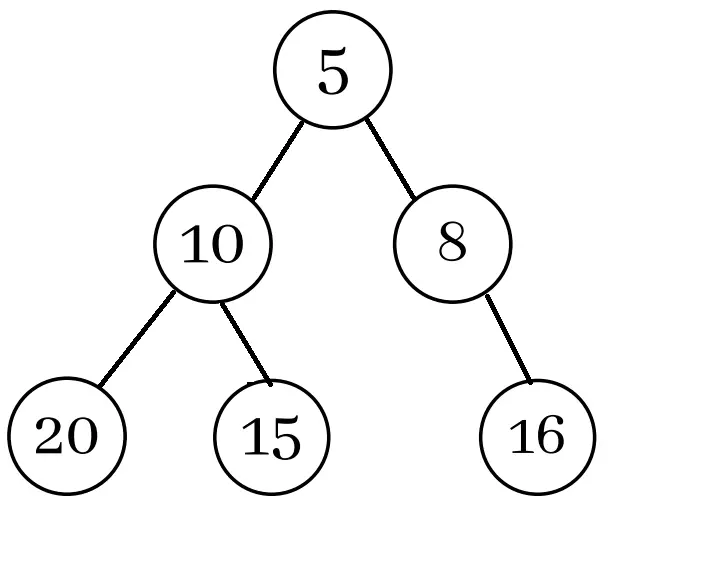
Every parent node is smaller than or equal to the child node in a Min Heap. It follows the ascending order, and the priority is always with the smaller node.

For a given node n, its left child will be at 2n+1 and the right at 2n+2.

See the following image.

In Python, the Min Heap can be implemented in two ways. These are discussed below.

Create a Class to Implement Min Heap in Python

We can create a class to implement the Min Heap in Python. We will initiate the class object with the size of the heap and define methods to carry out the insertion process of elements and map them to their respective indexes.

Example:

import sys


class min_heap:
    def __init__(self, size):
        self.storage = [0] * size
        self.size = size
        self.heap_size = 0
        self.Heap = [0] * (self.size + 1)
        self.Heap[0] = sys.maxsize * -1
        self.parent = 1
        self.root = 1

    def parent_idx(self, idx):
        return (idx - 1) // 2

    def lf_child_idx(self, idx):
        return 2 * idx + 1

    def rt_child_idx(self, idx):
        return 2 * idx + 2

    def has_parent(self, idx):
        return self.parent_idx(idx) >= 0

    def insert(self, idx):
        if self.heap_size >= self.size:
            return
        self.heap_size += 1
        self.Heap[self.heap_size] = idx
        heap = self.heap_size
        while self.Heap[heap] < self.Heap[heap // 2]:
            self.swap(heap, heap // 2)
            heap = heap // 2

    def swap(self, left, right):
        self.Heap[left], self.Heap[right] = self.Heap[right], self.Heap[left]

    def print_heap(self):
        for i in range(1, (self.heap_size // 2) + 1):
            print(
                "Parent:",
                str(self.Heap[i]),
                "Lt: " + str(self.Heap[2 * i]),
                "Rt: ",
                str(self.Heap[2 * i + 1]),
            )


min_heap = min_heap(10)
min_heap.insert(5)
min_heap.insert(1)
min_heap.insert(8)
min_heap.insert(2)
min_heap.insert(3)
min_heap.insert(7)
min_heap.insert(9)
min_heap.insert(6)
min_heap.insert(10)
min_heap.print_heap()

Output:

Parent: 1 Lt: 2 Rt:  7
Parent: 2 Lt: 5 Rt:  3
Parent: 7 Lt: 8 Rt:  9
Parent: 5 Lt: 6 Rt:  10

The insert() method adds elements to the heap. The index and order of the elements are managed using the swap() method that uses the rt_child_index() and lt_child_index() functions to adjust the levels of the child nodes based on the value of parent nodes.

The Min Heap is iterated over and displayed in a sequence using the class’s print_heap() function.

Use the heapq Module to Implement Min Heap in Python

Python provides a heapq module that can implement the heap data structure without creating other classes. This module ensures that the smallest element of the heap is popped every time to maintain the Min Heap structure.

We will use a list to maintain the nodes of the heap. The elements are added using the heappush() function, and it maintains the order accordingly so that the structure of Min Heap is maintained.

The heappop() pops the smallest element from the heap, the root node.

Example:

import heapq as heap

lst = []
heap.heappush(lst, 7)
heap.heappush(lst, 1)
heap.heappush(lst, 5)
heap.heappush(lst, 4)
heap.heappush(lst, 8)
heap.heappush(lst, 3)
print("Heap: ", lst)
print("Parent Node: ", heap.heappop(lst))
print("Child Nodes: ", lst)

Output:

Heap:  [1, 4, 3, 7, 8, 5]
Parent Node:  1
Child Nodes:  [3, 4, 5, 7, 8]

In the above example, we used a list lst to maintain the heap. The elements are added, and their order is automatically adjusted with the heappush() function.

The Min Heap is displayed. The parent node is popped using the heappop() method and is displayed.

The remaining child nodes are also displayed after removing the parent node.