How to Implement Low Pass Filter in Python
A low pass filter is a term that is among the basics of signal processing and is used quite often to filter signals to get more accurate results.
This tutorial will discuss the low-pass filter and how to create and implement it in Python.
A low-pass filter is utilized to pass a signal that has a frequency lower than the cut-off frequency, which holds a certain value specified by the user. All the signals with frequencies more than the cut-off frequency enervated.
Use Scipy to Create a Low-Pass Butterworth Filter in Python
In Python, we can utilize functions from the SciPy library to create a low-pass filter. SciPy, an abbreviation for Scientific Python, is a library that is utilized for supplying functions that carry out signal processing, optimization, and statistics. This library also uses the NumPy library underneath.
There are a couple of low-pass filters that exist in the real world. However, we will create a Butterworth low-pass filter in Python, as it has a maximally flat frequency, meaning no ripples in the passband. This makes it one of the most popular and used low-pass filters.
To successfully implement this method in Python, we will first need to import NumPy, SciPy, and Matplotlib modules to the python code.
The following code uses the SciPy module to create a low-pass Butterworth filter in Python.
import numpy as np
from scipy.signal import butter, lfilter, freqz
import matplotlib.pyplot as plt
def butter_lowpass(cutoff, fs, order=5):
nyq = 0.5 * fs
normal_cutoff = cutoff / nyq
b, a = butter(order, normal_cutoff, btype="low", analog=False)
return b, a
def butter_lowpass_filter(data, cutoff, fs, order=5):
b, a = butter_lowpass(cutoff, fs, order=order)
y = lfilter(b, a, data)
return y
# Setting standard filter requirements.
order = 6
fs = 30.0
cutoff = 3.667
b, a = butter_lowpass(cutoff, fs, order)
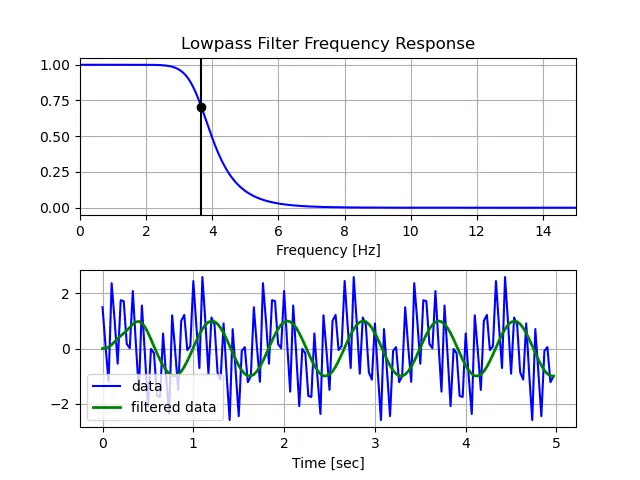
# Plotting the frequency response.
w, h = freqz(b, a, worN=8000)
plt.subplot(2, 1, 1)
plt.plot(0.5 * fs * w / np.pi, np.abs(h), "b")
plt.plot(cutoff, 0.5 * np.sqrt(2), "ko")
plt.axvline(cutoff, color="k")
plt.xlim(0, 0.5 * fs)
plt.title("Lowpass Filter Frequency Response")
plt.xlabel("Frequency [Hz]")
plt.grid()
# Creating the data for filteration
T = 5.0 # value taken in seconds
n = int(T * fs) # indicates total samples
t = np.linspace(0, T, n, endpoint=False)
data = (
np.sin(1.2 * 2 * np.pi * t)
+ 1.5 * np.cos(9 * 2 * np.pi * t)
+ 0.5 * np.sin(12.0 * 2 * np.pi * t)
)
# Filtering and plotting
y = butter_lowpass_filter(data, cutoff, fs, order)
plt.subplot(2, 1, 2)
plt.plot(t, data, "b-", label="data")
plt.plot(t, y, "g-", linewidth=2, label="filtered data")
plt.xlabel("Time [sec]")
plt.grid()
plt.legend()
plt.subplots_adjust(hspace=0.35)
plt.show()
Vaibhhav is an IT professional who has a strong-hold in Python programming and various projects under his belt. He has an eagerness to discover new things and is a quick learner.
LinkedIn