How to Plot Fast Fourier Transform (FFT) in Python

1. Use the Python scipy.fft Module for Fast Fourier Transform
2. Use the Python numpy.fft Module for Fast Fourier Transform

In this Python tutorial article, we will understand Fast Fourier Transform and plot it in Python.

Fourier analysis conveys a function as an aggregate of periodic components and extracting those signals from the components. When both the function and its transform are exchanged with the discrete parts, then it is expressed as Fourier Transform.

FFT works majorly with computational algorithms for increasing the execution speed. Filtering algorithms, multiplication, image processing are a few of its applications.

Use the Python scipy.fft Module for Fast Fourier Transform

One of the most important points to take a measure of in Fast Fourier Transform is that we can only apply it to data in which the timestamp is uniform. The scipy.fft module converts the given time domain into the frequency domain. The FFT of length N sequence x[n] is calculated by the fft() function.

For example,

from scipy.fftpack import fft
import numpy as np

x = np.array([4.0, 2.0, 1.0, -3.0, 1.5])
y = fft(x)
print(y)

Output:

[5.5       -0.j         6.69959347-2.82666927j 0.55040653+3.51033344j
 0.55040653-3.51033344j 6.69959347+2.82666927j]

We can also use noisy signals as they require high computation. For example, we can use the numpy.sin() function to create a sine series and plot it. For plotting the series, we will use the Matplotlib module.

See the following example.

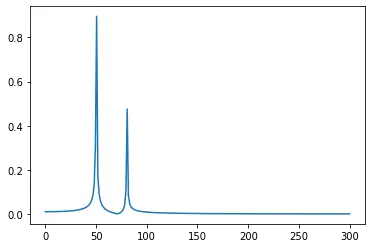
import scipy.fft
import matplotlib.pyplot as plt
import numpy as np


N = 500
T = 1.0 / 600.0
x = np.linspace(0.0, N * T, N)
y = np.sin(60.0 * 2.0 * np.pi * x) + 0.5 * np.sin(90.0 * 2.0 * np.pi * x)
y_f = scipy.fft.fft(y)
x_f = np.linspace(0.0, 1.0 / (2.0 * T), N // 2)

plt.plot(x_f, 2.0 / N * np.abs(y_f[: N // 2]))
plt.show()

Note that the scipy.fft module is built on the scipy.fftpack module with more additional features and updated functionality.

Use the Python numpy.fft Module for Fast Fourier Transform

The numpy.fft works similar to the scipy.fft module. The scipy.fft exports some features from the numpy.fft.

The numpy.fft is considered faster when dealing with 2D arrays. The implementation is the same.

For example,

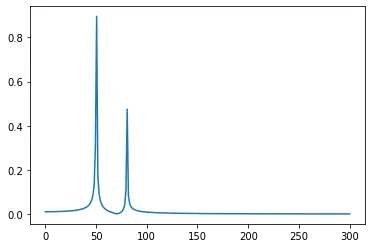
import matplotlib.pyplot as plt
import numpy as np

N = 500
T = 1.0 / 600.0
x = np.linspace(0.0, N * T, N)
y = np.sin(60.0 * 2.0 * np.pi * x) + 0.5 * np.sin(90.0 * 2.0 * np.pi * x)
y_f = np.fft.fft(y)
x_f = np.linspace(0.0, 1.0 / (2.0 * T), N // 2)

plt.plot(x_f, 2.0 / N * np.abs(y_f[: N // 2]))
plt.show()