How to Round an Average to 2 Decimal Places in PostgreSQL

1. Use the AVG() Function to Get the Average of a Set in PostgreSQL
2. Use the ROUND Function to Round an Average to 2 Decimal Places

Today, we will learn to round an average to 2 decimal places in PostgreSQL.

Use the AVG() Function to Get the Average of a Set in PostgreSQL

The AVG() function gives the average in PostgreSQL. This is an aggregate function that allows us to calculate the average value.

Syntax:

AVG(Column_Name)

Suppose we want to calculate the average of a column in a table CAT having IDs and names. Then, we can do this as shown below.

SELECT AVG(Name) from CAT;

This will return the average of the values inside the table CAT column.

Let us see how to round off the average values obtained to different decimal places.

Use the ROUND Function to Round an Average to 2 Decimal Places

The ROUND function is given under the MATHEMATICAL FUNCTIONS AND OPERATORS heading in the PostgreSQL documentation. Mathematical functions return the same data type as provided in their arguments.

The ROUND function comes with two different syntaxes.

Syntax 1:

ROUND(dp or numeric)

Syntax 2:

ROUND(v numeric, s int)

The first query type tends to round off to the nearest integer, meaning you cannot provide custom decimal places. So if you call the ROUND function on 42.4, it will return 42.

DP in the argument stands for double-precision if you provide a decimal place argument in the function. The numeric type can be of 2-, 4-, and 8-byte floating-point numbers or those with a selectable precision.

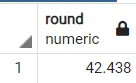
The second function also takes into consideration the decimal places you might want to round to, so if you call a function to round the number 42.4382 to 3 decimal places, you can write a query like:

select ROUND(42.4382, 3)

Output:

You can also see that running the following:

select ROUND(42.5)

It will return 43 as an integer rounding up with a 0.5 tends to round to the ceiling part of the nearest integer. The floor integer would be 42, and the ceiling part would be 43.

Now, let’s make a table and see how we can run the following. Let us define a table STUDENT with the two columns, ID and CGPA.

CREATE TABLE student (
                       ID int PRIMARY KEY,
                       CGPA float8
)

Now let’s call the INSERT statement to enter some values into this newly-created table.

insert into student values (1, 2.3), (2, 4), (3, 4) , (4, 3.76)

Suppose we want to get the AVERAGE of all CGPAs listed in this table. Using the INTEGER argument would lead to us having an inaccurate answer.

So we can run a query as:

select round(avg(CGPA), 2)
from student

Why did we use 2? Because it is the greatest number of decimal places in all of our CGPAs.

And we can get a pretty accurate answer using this number to round off. But why is there an error?

Output:

ERROR:  function round(double precision, integer) does not exist
LINE 10: select round(avg(CGPA), 2)

The former ROUND statement allows DP (Double Precision), but the latter query syntax does not.

You can only use a numeric with up to 131072 digits before the decimal point in that function. And up to 16383 digits after.

Hence, float8 does not work, so you run into a syntax error.

Use CAST to Remove Syntax Errors for Rounding in PostgreSQL

In the previous solution, we ran into a problem where the latter syntax for ROUND did not support the float or double precision type. So to run the query, we can CAST to numeric as a possible solution.

As we know, numeric can have approximately 17000 digits after the decimal point. We can go ahead and use the CAST effectively.

select round(avg(CGPA)::numeric, 2)
from student

This will return 3.52, the exact result of rounding off the set of CGPAs. Another syntax that we can use for CAST is:

select round(CAST(avg(CGPA) as numeric), 2)
from student

Use TO CHAR for Better Decimal Formatting and Rounding in PostgreSQL

Another handy workaround to rounding any number in PostgreSQL is using the TO_CHAR function. It is present under the DATA TYPE FORMATTING FUNCTIONS classification in PostgreSQL.

It helps convert various data types to strings and vice versa. We can use the following syntaxes to convert to a custom decimal place.

to_char ( numeric_type, text ) ? text

to_char(125, '999') ? 125

to_char(125.8::real, '999D9') ? 125.8

to_char(-125.8, '999D99S') ? 125.80-

The second argument that you can see above helps define the template we round our number and print its output. So if we want to round off a number to specific decimal places, we can define the template as one of the following.

1. FM (prefix) - fill mode (suppress leading zeroes and padding blanks), FMMonth
2. TH (suffix) - upper case ordinal number suffix, DDTH, e.g., 12TH
3. the (suffix) - lower case ordinal number suffix, DDth, e.g., 12th
4. FX (prefix) - fixed format global option (see usage notes), FX Month DD Day
5. TM (prefix) - translation mode (use localized day and month names based on lc_time), TMMonth
6. SP (suffix) - spell mode (not implemented), DDSP

Using the TO_CHAR function, let’s round off the number 352.45 using the TO_CHAR function.

select to_char(352.45, 'FM999D9')

Output:

352.5

So that means that this works correctly. But you might be wondering, what are the D and the FM that we appended to the integer?

The D represents the trailing decimal places and defines the number of values the query will round it off into.

The FM stands for FILL MODE. It removes all blanks and leading zeroes.

If you do not put the FM before it, it will give an output like this.

Output:

"[........] 352.5"

So putting the FM removes the invalid characters before our rounded-up result.

Use a Custom Overloaded Function for ROUND in PostgreSQL

Another way to round off an average, which might have a float type not supported by the original ROUND function, can be to make a function that can overload this. Then CAST the provided argument in float type to numeric for ROUND to work.

This function will call ROUND again, but CAST is the first argument passed to numeric.

Example:

create function ROUND(num float, decim_places int) returns NUMERIC as $f$
 select ROUND(num::numeric, decim_places)
$f$ language SQL immutable

We then call the ROUND function as follows.

select ROUND(avg(cgpa), 2) from student

And this will now return the correct result without any means of CASTING in our query.

The ROUND overloaded function takes two parameters, one is a float, and the other is an int. This function returns a numeric data type officially returned by the SELECT ROUND() operation that casts the NUM parameter into numeric.

Why did we use the IMMUTABLE keyword in the function? A function can be defined using the IMMUTABLE, STABLE, or VOLATILE keywords.

The IMMUTABLE attribute means that if a function is given the same parameters constantly, it will not call the function but rather return the constant function value.

If you look under the FUNCTION VOLATILITY CATEGORIES classification of the PostgreSQL documentation, you’ll notice a pretty good example of the IMMUTABLE keyword.

If you run the query above,

SELECT Round(3.52, 1)

It returns 3.5 once; then, the function won’t run the query if you call it again. It instead returns 3.5 as itself as the parameters are unchanged.

The default for any of these functions is VOLATILE if no such attribute is defined while creating the function.

Modifications to the Created ROUND Function in PostgreSQL

The ROUND function we created above can be modified to give us better-looking results using accuracy values.

Suppose we want to round off 21.56 to an accuracy of 0.05; how would the answer come out?

If we don’t define an accuracy, the ROUND function with just 21.56 will return 22. However, with an accuracy of 0.05, there might be a (+- 0.05) value error that we need to resolve.

An excellent method of doing this would be to divide the number by the accuracy value defined, which is 0.05, round off the answer we get, and then multiply it by 0.05 (accuracy value) again.

So if we want to round off 21.56 with a better estimate, we could say:

21.56/0.05 = 431.2

Using the value 431.2, we can round this to 431 and then multiply it by 0.05 to get the answer 21.55, rounded perfectly without the error (+- 0.05).

In case we want the answer within one decimal place, we could assume an error of (+- 0.5) and then do the following:

21.56/0.5 = 43.12

Rounding this would give 43, multiplied by 0.5 to get the rounded-off value at 21.5. This is perfectly fine since there is an estimated error, and (21.56 ~~ 21.6) would be incorrect in this manner.

Now that you understand how accuracy works let’s define a function again using ROUND to return the correct value. We will be passing two parameters, one being the number we want to round off and the other being the accuracy value.

The rest of the function will follow the same syntax as provided above.

create function ROUND(num float, acc float) returns FLOAT as $f$
	select ROUND(num/acc)*acc
$f$ language SQL immutable

So when you run the query with an accuracy value of 0.05,

select ROUND(avg(cgpa), 0.02::float8) from student

Output:

3.52 (double precision)

We used the FLOAT8 casting to be on the safe side; if we had another function with the same number of parameters, we could confuse our PostgreSQL database.

Performance Claims in ROUND Overloading in PostgreSQL

This section has been added to understand the best options available for ROUND.

We’ll add an abstract for this so they can skim and go about it. However, developers who require efficient and faster solutions can go ahead and read the explanations in detail.

• Function Overload is faster than CAST encoding for ROUND.
• SQL may overrun PLPGSQL in performance when combined with JIT optimization.

There were two ways to round for float or double precision. One was the standard CAST, and the other was the FUNCTION OVERLOAD.

An email from Brubaker Shane to PostgreSQL found here states that using the CAST operator makes a considerable difference in performance and if you turn off the SEQ SCANS, the cost gets 7x higher. Compare this to the FUNCTION OVERLOAD, and you’ll notice that the latter is better.

FUNCTION OVERLOAD with attributes such as STABLE or IMMUTABLE tend to decrease the overhead that comes with running functions, significantly increasing the performance and leading to fewer issues over time.

If constant parameters are called every time, the query doesn’t have to be run repeatedly. Instead, the function value is returned as it is for the same values.

In our functions here, we used the language SQL rather than PLPGSQL, which can also be used. If we were to increase performance, why did we use SQL rather than PLPGSQL?

The PostgreSQL documentation states that PLPGSQL is a much better procedural way of computations. Why?

Where SQL would send the queries incrementally, process them, wait, and then compute before sending the other query, PLPGSQL would group these computations and reduce the multiple parsing that SQL tends to do.

In that case, PLPGSQL seems like a perfect option for decreasing overhead. However, SQL tends to work better with JIT OPTIMIZATION.

JIT stands for JUST-IN-TIME, which means it evaluates the queries at run-time that the CPU can execute at the earliest to save time. JIT accelerated operations use inlining to reduce the overhead in functional calls.

JIT would inline the bodies of these functions into different expressions that can then be executed. And, of course, this would reduce the performance overhead.

JIT OPTIMIZATION uses an LLVM infrastructure in our PostgreSQL database. And in the TRANSFORM PROCESS section of the LLVM documentation, you can see how optimization works and efficiently produces results.

ROUND With Different Numeric Representations in PostgreSQL

Float is a binary representation. If you remember, you will realize that float comes with a Mantissa, a number expression preceded either with an exponential increase/decrease or a sign before it.

Float is rounded in three different modes:

ROUND TOWARDS ZERO: 1.5 to 1 (truncate extra digits)
ROUND HALF-WAY FROM ZERO: 1.5 to 2 (if fraction equal to half of the base, go forward to the nearest integer)
ROUND HALF TO EVEN (Banker's ROUND): 1.5 to 2 but 2.5 to 2 (we always round off to even, resulting in case of half base to reduce errors)

Let’s begin by rounding off a decimal floating point. This rounding-off is simple and follows a basic syntax of rounding to the nearest integer at half the base.

Before we begin, you must clearly understand the formulae used to round off different numeric representations; DECIMAL, BINARY, and HEXA-DECIMAL. We will use a standardized IBM-provided formula with varying values of RADIX (number-base).

Formula:

sign(x)* ( b(e-n) ) * floor( abs(x) * ( b(n-e) ) + 1/2

In this formula, b stands for the base. e stands for the EXPONENT of the value we want to ROUND off.

And ABS stands for absolute, a positive numeric representation. FLOOR stands for the preceding nearest integer.

FLOOR of 2.5 would be 2, and CEILING would be 3.

Hence using the different RADIX values will give different answers for each representation. If we round off 3.567 in decimal notation, we will get:

 3.6 for decimal digit = 1

Using BINARY, we would get:

3.6 for decimal digit = 3/4

And using hexadecimal,

3.6 for decimal digit = 1/2

Hence, we can now create a function for these different numeric representations.

For our decimal cases, we will call the ROUND function. However, we will change our statements for binary and hexadecimal.

For both, we’ll first split our number into two different parts, one before the decimal and the other after the decimal part.

If the digits to round off are less than the most significant bits, we’ll truncate our value to the difference between BIN_BITS and the digit that we rounded off. Else, we’ll truncate those digits.

CREATE FUNCTION trunc_bin(x bigint, t int) RETURNS bigint AS $f$
    SELECT ((x::bit(64) >> t) << t)::bigint;
$f$ language SQL IMMUTABLE;

CREATE FUNCTION ROUND(
    x float,
    xtype text,  -- 'bin', 'dec' or 'hex'
    xdigits int DEFAULT 0
)
RETURNS FLOAT AS $f$
    SELECT CASE
        WHEN xtype NOT IN ('dec','bin','hex') THEN 'NaN'::float
        WHEN xdigits=0 THEN ROUND(x)
        WHEN xtype='dec' THEN ROUND(x::numeric,xdigits)
        ELSE (s1 ||'.'|| s2)::float
        END
    FROM (
        SELECT s1,
            lpad(
                trunc_bin( s2::bigint, CASE WHEN xd<bin_bits THEN bin_bits - xd ELSE 0 END )::text,
                l2,
                '0'
            ) AS s2
        FROM (
             SELECT *,
                (floor( log(2,s2::numeric) ) +1)::int AS bin_bits, -- most significant bit position
                CASE WHEN xtype='hex' THEN xdigits*4 ELSE xdigits END AS xd
            FROM (
                SELECT s[1] AS s1, s[2] AS s2, length(s[2]) AS l2
                FROM (SELECT regexp_split_to_array(x::text,'\.')) t1a(s)
             ) t1b
        ) t1c
    ) t2
$f$ language SQL IMMUTABLE;

Hence, we can use this to call ROUND on any numeric representation possible.

Use TRUNC for Rounding Display in PostgreSQL

Another function that you can use is the TRUNC method which cuts off the value at a specific mark.

So calling TRUNC on 42.346 at position 2 will make it:

42.34

If you need to round to the nearest FLOOR integer, you can use TRUNC as follows:

SELECT TRUNC(42.346, 2)