How to Curve Curvature in Python

Curvature is a measure of deviance of a curve from being a straight line. For example, a circle will have its curvature as the reciprocal of its radius, whereas straight lines have a curvature of 0.

In this tutorial, we will learn how to calculate the curvature of a curve in Python using numpy module. We will calculate other quantities also like velocities, acceleration, and more. You can find the necessary formulas for them in the picture below.

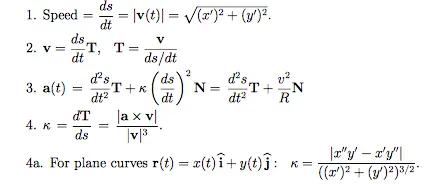
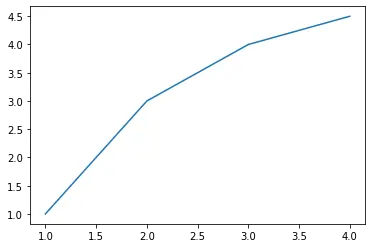
We will work with the following curve.

import numpy as np
import matplotlib.pyplot as plt

coordinates = np.array(
    [[1, 1], [1.5, 2], [2, 3], [2.5, 3.5], [3, 4], [3.5, 4.25], [4, 4.5]]
)

plt.plot(coordinates[:, 0], coordinates[:, 1])

Output:

For such problems related to curves, we need to be to calculate the derivates of the given curve at each point. The numpy.gradient() method is used for such cases, which returns the gradient of an N-Dimensional array.

In the following code, we calculate the velocity for the curve at all points.

x_t = np.gradient(coordinates[:, 0])
y_t = np.gradient(coordinates[:, 1])

vel = np.array([[x_t[i], y_t[i]] for i in range(x_t.size)])

print(vel)

Output:

[[0.5   1.   ]
 [0.5   1.   ]
 [0.5   0.75 ]
 [0.5   0.5  ]
 [0.5   0.375]
 [0.5   0.25 ]
 [0.5   0.25 ]]

After calculating velocity we proceed to the speed. Now the speed is the modulus of the velocity. However, it should be known that till now everything is a function of t (t represents time interval). Thus, we will represent speed as a numpy array of values at each of the one-second time intervals.

See the code below.

speed = np.sqrt(x_t * x_t + y_t * y_t)

print(speed)

Output:

[1.11803399 1.11803399 0.90138782 0.70710678 0.625      0.55901699
 0.55901699]

Now for calculating the tangent, we will perform some transformation which will ensure that the size of the speed and velocity is the same. Also, we need to be able to divide the vector-valued velocity function to the scalar speed array.

tangent = np.array([1 / speed] * 2).transpose() * vel

print(tangent)

Output:

[[0.4472136  0.89442719]
 [0.4472136  0.89442719]
 [0.5547002  0.83205029]
 [0.70710678 0.70710678]
 [0.8        0.6       ]
 [0.89442719 0.4472136 ]
 [0.89442719 0.4472136 ]]

Similarly, we can now isolate the components of the tangent and compute its gradient to find the normal vector also.

We will now implement the provided formula of curvature in the code below.

ss_t = np.gradient(speed)
xx_t = np.gradient(x_t)
yy_t = np.gradient(y_t)

curvature_val = np.abs(xx_t * y_t - x_t * yy_t) / (x_t * x_t + y_t * y_t) ** 1.5

print(curvature_val)

Output:

[0.         0.04472136 0.17067698 0.26516504 0.256      0.17888544
 0.        ]