How to Use Recursion to Draw Koch Snowflake in Java

This article will explain how to make a Koch snowflake using recursion in Java.

Use Recursion to Draw Koch Snowflake in Java

The Koch curve is also known as a Snowflake curve since it is formed like a snowflake. One of the fractal curves is this one.

The following is the specific drawing method.

1. Divide each side of an equilateral triangle into three equal sections.
2. Delete the middle section after taking the trisection of one side of the middle section for the side to construct an equilateral triangle.
3. Draw a smaller triangle by repeating the first two steps.
4. Continue until you reach infinity, and the curve that results is a Koch curve.

Let’s look at an example. A little cluster of broccoli may be seen as a branch of the larger cluster, which exhibits a self-similar form at different scales.

The smaller branches may be extended to the proper proportions to create a cluster almost identical to the whole. As a result, we may argue that such a broccoli cluster is fractal.

The following are some properties of a fractal:

1. The fractal set contains a fine structure or scale features at any tiny size.
2. It is too irregular to be represented in classical Euclidean geometry.
3. The self-similar Hausdorff dimension will be bigger than the topological dimension, at least roughly or arbitrarily.

Traditional geometric vocabulary is unable to explain the fractal set. It is neither the path of points that meet specific criteria nor the set of solutions to a few basic equations.

Self-similarity exists in the fractal set, whether approximation self-similarity or statistical self-similarity. In most cases, a fractal set’s fractal dimension is higher than its equivalent topological dimension.

A relatively simple procedure defines the fractal set in the most compelling circumstances, and it may be created as an iteration of the transformation.

Various graphs call recursive implementation according to different drawing techniques, such as the Koch curve.

Study this code’s algorithm and use it as a model for other Java applets.

The recursive Serpienski Gasket was the primary reference for this recursive Koch snowflakes program, and the formula below was used to create the source code.

Source code:

package KochSnowflakes;
import java.awt.*;
import javax.swing.*;
public class RecursiveKochSnowFlakes extends JApplet {
  int initiallevel = 0;
  public void init() {
    String StringLevel = JOptionPane.showInputDialog("Enter the Recursion Depth");
    initiallevel = Integer.parseInt(StringLevel);
  }
  public void paint(Graphics z) {
    DrawKoch(z, initiallevel, 20, 280, 280, 280);
    DrawKoch(z, initiallevel, 280, 280, 150, 20);
    DrawKoch(z, initiallevel, 150, 20, 20, 280);
  }
  private void DrawKoch(Graphics z, int level, int a1, int b1, int a5, int b5) {
    int delX, delY, a2, b2, a3, b3, a4, b4;
    if (lev == 0) {
      z.drawLine(a1, b1, x5, y5);
    } else {
      delX = a5 - a1;
      delY = b5 - b1;
      a2 = a1 + delX / 3;
      b2 = b1 + delY / 3;
      a3 = (int) (0.5 * (a1 + a5) + Math.sqrt(3) * (b1 - b5) / 6);
      b3 = (int) (0.5 * (b1 + b5) + Math.sqrt(3) * (a5 - a1) / 6);
      a4 = a1 + 2 * delX / 3;
      b4 = b1 + 2 * delY / 3;
      DrawKoch(z, level - 1, a1, b1, a2, b2);
      DrawKoch(z, level - 1, a2, b2, a3, b3);
      DrawKoch(z, level - 1, a3, b3, a4, b4);
      DrawKoch(z, level - 1, a4, b4, a5, b5);
    }
  }
}

Outputs:

• If we input 0 as the depth of recursion,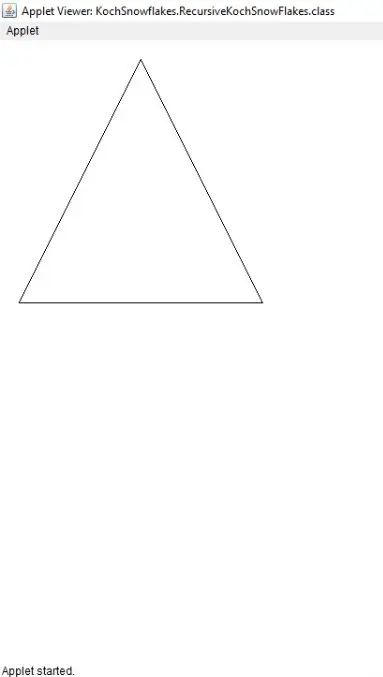

  

• If we input 1 as the depth of recursion,

  

• If we input 2 as the depth of recursion,

  

• If we input 3 as the depth of recursion,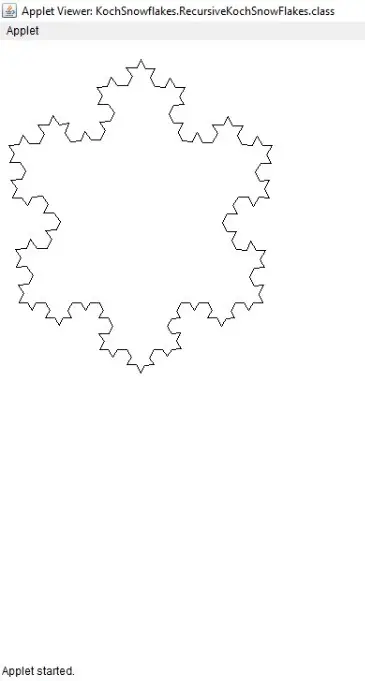

  

• If we input 4 as the depth of recursion,