How to Print Binary Tree in Python

1. Binary Tree in Python
2. Traversal Order of a Tree
3. Implementation of Binary Tree in Python
4. Print the Whole Binary Tree Using Python

This article will discuss a binary tree and how we can use it. We will also see how we can print it using Python.

We will learn about the terminologies used in working on binary trees. We will also look into an example of a binary tree using Python code.

Binary Tree in Python

Python’s binary trees are one of the most efficient data structures available, and they’re also relatively simple to implement. A binary tree is a tree-like data structure with a root node and two child nodes, a left and a right.

Each node can have any number of child nodes. This article will look at how to create and traverse a binary tree in Python.

Let’s get a better understanding of the terminology associated with the tree.

1. Root: The topmost node of a tree without a parent. Every tree has one root.
2. Edge: Edge is a parent-child link.
3. Leaf: A node without children. The tree’s final node. Trees have multiple leaf nodes.
4. Subtree: The tree uses a node as its root.
5. Depth: Depth is the node’s distance from the root.
6. Height: The node’s height is the distance to the subtree’s deepest node.
7. Height of the Tree: The tree’s height is the highest node and corresponds to the same height as the root node.

Traversal Order of a Tree

The tree is traversed by starting at the root node and visiting the left and right child nodes. The order in which the nodes are visited is called the traversal order.

In-order Traversal Tree

There are several different ways to traverse a binary tree. The most common is the in-order traversal, which visits the left, root, and right child nodes.

Pre-order Traversal Tree

Another standard traversal is the pre-order traversal, which visits the root node first, then the left child, and finally the right child.

The in-order traversal is the most efficient way to visit all the nodes in a binary tree since it visits each node only once. The pre-order traversal is a little less efficient since it calls the root node twice.

However, the pre-order traversal is often used when we want to modify the tree during the traversal since it’s easy to alter the root node first and then the left and right child nodes.

Here’s a syntax and simple implementation of the in-order traversal in Python.

def inorder(node):
    if node is not None:
        inorder(node.left)
        print(node.val)
        inorder(node.right)

So, this is how we code when we want to use the in-order traversal method.

And here’s the pre-order traversal:

def preorder(node):
    if node is not None:
        print(node.val)
        preorder(node.left)
        preorder(node.right)

Post-order Traversal

We can also traverse the tree in post-order, which visits the left child, the right child, and then the root node. However, post-order traversal is less common since it’s less efficient than the other two traversals.

There are other ways to traverse a binary tree, such as the level-order traversal, which visits the nodes in the tree level by level. However, we won’t be covering that traversal in this article.

Now that we’ve seen how to traverse a binary tree let’s look at how to create one binary tree and print it using Python.

Implementation of Binary Tree in Python

We know what a binary tree is and the terminology connected with it. We will implement the binary tree using Python to understand better how the binary tree works.

All we have to do is copy that code here and write new code in it. Because it’s part of the binary tree, we must write the new code with the already written codes.

Example code:

class binaryTreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def printTree(root):
        print(root.data)
        print("L", root.left.data, end=": ")
        print("R", root.right.data, end=": ")


bnt1 = binaryTreeNode(1)
bnt2 = binaryTreeNode(2)
bnt3 = binaryTreeNode(3)
bnt1.left = bnt2
bnt1.right = bnt3
bnt2.left = bnt1
bnt2.right = bnt3
bnt3.left = bnt1
bnt3.right = bnt2

The method def printTree(root) gives us the root. Because when we have the root of the tree, we can access the entire tree with the nodes.

After declaring the method, we will check some conditions. We can see the method def PrintTree(root) in the code above.

Let’s try printing root 1, bnt1, to see what we get.

Example code:

print(bnt1.printTree())

Output:

1
L 2: R 3: None

The output shows that the tree contains two nodes (the left node and the right node). The data in the left node is 2, and in the right node is 3.

We can also print bnt2 and bnt3 to see what data points they contain.

Print the Whole Binary Tree Using Python

Here is the entire Binary Tree. We can run it and learn more about how a binary tree is printed using Python with the random library of Python.

import random


class BinaryTree:
    def __init__(self, key):
        self.key = key
        self.right = None
        self.left = None

    def insert(self, key):
        if self.key == key:
            return
        elif self.key < key:
            if self.right is None:
                self.right = BinaryTree(key)
            else:
                self.right.insert(key)
        else:  # self.key > key
            if self.left is None:
                self.left = BinaryTree(key)
            else:
                self.left.insert(key)

    def display(self):
        lines, *_ = self._display_aux()
        for line in lines:
            print(line)

    def _display_aux(self):
        """Returns list of strings, width, height, and horizontal coordinate of the root."""
        # No child.
        if self.right is None and self.left is None:
            line = "%s" % self.key
            width = len(line)
            height = 1
            middle = width // 2
            return [line], width, height, middle
        # Only left child.
        if self.right is None:
            lines, n, p, x = self.left._display_aux()
            s = "%s" % self.key
            u = len(s)
            first_line = (x + 1) * " " + (n - x - 1) * "_" + s
            second_line = x * " " + "/" + (n - x - 1 + u) * " "
            shifted_lines = [line + u * " " for line in lines]
            return [first_line, second_line] + shifted_lines, n + u, p + 2, n + u // 2
        # Only right child.
        if self.left is None:
            lines, n, p, x = self.right._display_aux()
            s = "%s" % self.key
            u = len(s)
            first_line = s + x * "_" + (n - x) * " "
            second_line = (u + x) * " " + "\\" + (n - x - 1) * " "
            shifted_lines = [u * " " + line for line in lines]
            return [first_line, second_line] + shifted_lines, n + u, p + 2, u // 2
        # Two children.
        left, n, p, x = self.left._display_aux()
        right, m, q, y = self.right._display_aux()
        s = "%s" % self.key
        u = len(s)
        first_line = (x + 1) * " " + (n - x - 1) * "_" + s + y * "_" + (m - y) * " "
        second_line = (
            x * " " + "/" + (n - x - 1 + u + y) * " " + "\\" + (m - y - 1) * " "
        )
        if p < q:
            left += [n * " "] * (q - p)
        elif q < p:
            right += [m * " "] * (p - q)
        zipped_lines = zip(left, right)
        lines = [first_line, second_line] + [a + u * " " + b for a, b in zipped_lines]
        return lines, n + m + u, max(p, q) + 2, n + u // 2


b = BinaryTree(100)
for _ in range(100):
    b.insert(random.randint(50, 150))
b.display()

Output:

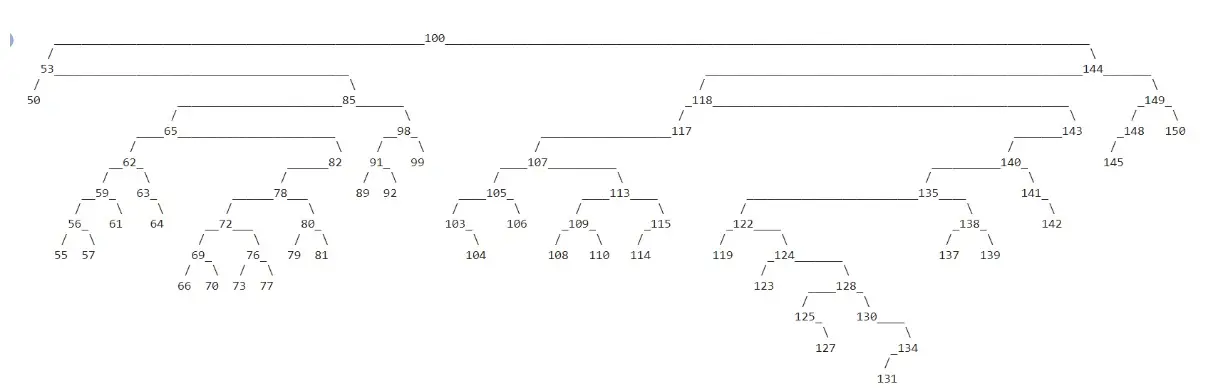
The output of the code keeps changing every time we run it. This is because we are using the random module of Python.

We hope you find this article helpful in understanding how to print a binary tree using Python.