Red-Black Tree in Java
- Red-Black Trees
- Determine The Balance of Red-Black Tree
- Subtree Rotation in a Red-Black Tree
- Searching Algorithm: Red-Black Tree
- Insertion: Red-Black Tree Java
- Summary
- References
This tutorial provides an up-to-date and in-depth examination of one of the most well-known data structure techniques, the red-black tree. Also, we execute a few Java demonstration programs on essential elements that we think are necessary for you to comprehend.
Although this article combines all the essential characteristics of a red-black tree, we aim to make it as easier as it could be. However, we also understand that it can be challenging for beginners to understand this topic.
Therefore, we recommend reading: Binary Search Trees.
Red-Black Trees
A red-black tree is a binary search tree unique in computer science, particularly in data structure and algorithms. We use it to group comparable data bits for complex problem statements.
The following table contains general information about a red-black tree.
| No. | Type of tree | Self branching, binary search tree |
|---|---|---|
| 1 | Creator | Rudolf Bayer |
| 2 | Functions | Searching, insertion, detection |
| 3 | Space complexity | O(n) |
| 4 | Time complexity | O(log n) |
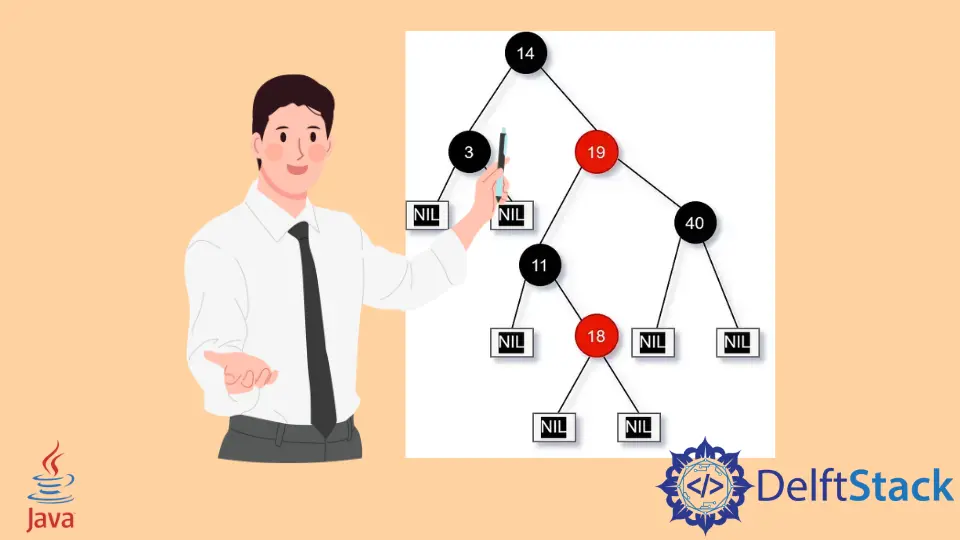
Figure 1: A typical red-black tree (Demonstration example).
Properties of Red-Black Tree
A red-black tree must satisfy the following conditions.
- Each node has a red or black color.
- We refer to the
NIL (= NONE)-"children"as leaves of the tree. - Every
NIL-leafis black. - The root of the tree must also be black.
- Suppose a node is red, then both the node’s children have to be black.
- All paths from the node to descendant leaves must contain the same number of black nodes for each node.
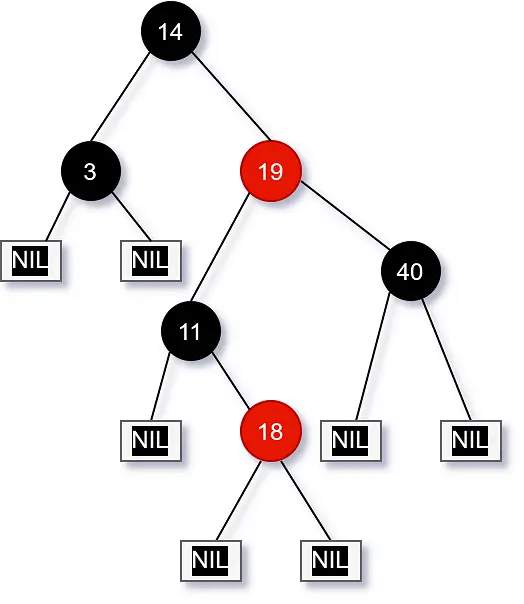
Height Defined of Red-Black Tree
Figure 2: Black height of the tree.
Attributes of the Nodes in the Tree
The tree nodes should contain the following attributes.
- color
- key
- Left Child
- Right Child
- Parent (excluding root node)
Here is how we will approach nodes in a Java program later.
// class node
public class BlackRedTreeNode {
int Ndata; // The data of the node
BlackRedTreeNode P; // parent
BlackRedTreeNode L; // Left
BlackRedTreeNode R; // Right
int Nclr; // Color of the node
} // end of class
Determine The Balance of Red-Black Tree
We will hypothetically use a data structure algorithmic approach to solve the problem statement of how to balance the red and black tree structure.
The node color limitations ensure that any simple path from the root to a leaf is no longer than twice as long as any other such path. It adds to the red-black tree’s self-balancing ability.
- Height of the node:
Hn Tas Tree
You can see the edges of the longest path to a leaf.
- The black height of
node-x:
bh(x) represents the number of black nodes, including the nil [T] on the path from x to the leaf, not counting x, though.
- Nil Leaves:
These properties in the tree are there only for counting (Property Number 6).
-
Lemma: A red-black tree with
nnodes has height:
$$
≤ 2 log (n+1)
$$
-
Proof: The subtree rooted at any node
xcontains at least:
$$
2^bh(x) -1
$$
Therefore, the smallest subtree with the black height bh(x) and the complete tree has n internal nodes:
$$ 2^bh(root[T]) -1 ≤ n $$
$$ bh(root[T]) ≤ log (n+1) $$
Height (T) = number of edges on the longest path to the leaf
$$ ≤ 2 . bh (root[T]) $$
$$ ≤ 2 log (n+1) $$
Subtree Rotation in a Red-Black Tree
A rotation is a unique operation designed for self-balancing binary Search Trees that takes O(1) to finish. Furthermore, the same rotations help keep the in-order traverse of the keys.
Also, the positions of a subtree’s nodes are swapped during rotation operation. When other operations, such as insertion and deletion, violate the attributes of a red-black tree, the rotation operation is performed to restore them.
Rotations are classified into two types:
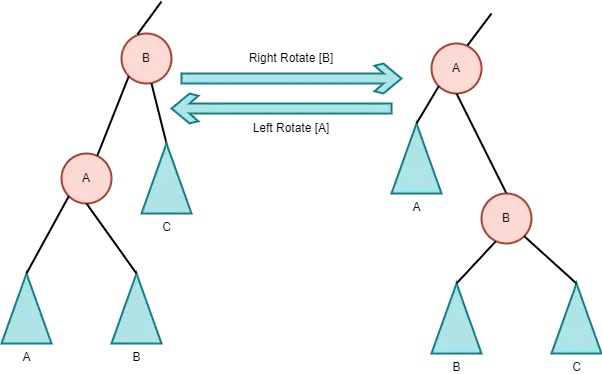
The aunt of the evaluated node influences the choice to do rotations or a color change (the current node). We rotate if the node has a Black Aunt.
If the node has a Red Aunt, we reverse the colors. We must color fix the tree after we rotate it.
Following those operations, the tree should be terminated, as shown below.
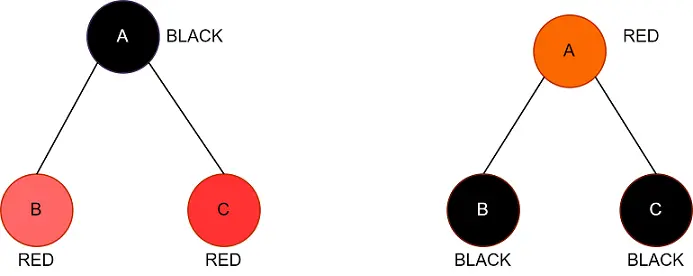
Example Java Code for the Right Rotation:
// function
// n as node
// P as Parent
// R as Right
// L as Left
// LC as LeftChild
private void RightRotation(TreeNode n) {
TreeNode paPrent = n.P;
TreeNode LC = n.L;
n.L = LC.R;
if (LC.R != null) {
LC.R.P = n;
}
LC.right = n;
n.P = LC;
Replace(P, n, LC);
} // end of function
Example of the Left Rotation in Java:
// function left rotation
private void LeftRotation(TreeNode n) {
TreeNode P = n.P;
TreeNode Rc = n.R;
n.R = Rc.L;
if (Rc.L != null) {
Rc.left.P = n;
}
Rc.left = n;
n.P = Rc;
replace(P, n, Rc);
} // end of function
Searching Algorithm: Red-Black Tree
The search works in the same way any binary search tree does. We begin by comparing the search key to the root.
If your search key is smaller, the search is continued in the left subtree; if the search key is more significant, the search is continued in the right subtree.
We repeat this process until we find the desired node that we want. In other words, until we reach a nil leaf point.
Suppose we reach a nil leaf, which means the key we’re looking for isn’t in the tree.
Code: Searching
// Sn as Search Nodes
// k as Key
// n as node
// r as Right
// d as Data of the data
// L as left
// Function starts here
public TreeNode Sn(int k) {
TreeNode n = r;
// determine the search by applying while loop
// loop starts
while (n != null) {
// checking the key
if (k == n.d) {
return n;
} else if (k < n.d) {
n = n.L;
} else {
n = n.R;
} // condition ends
} // loop ends
return null;
} // Function ends here
Insertion: Red-Black Tree Java
The following program demonstrates a function that we can use to insert nodes in a black-red tree. Though it follows the correct order as far as the data structure point of view is concerned, a complete execution will vary depending on your approach.
The following code is still enough for starters, especially for beginners.
Code: Insertion
// iN as insertion node
// k as key of the tree
// r as root of the node
// R as right node
// L as left node
// d as data
// p as parent
public void iN(int k) {
TreeNode n = r;
TreeNode P = null;
// Swaping the nodes
while (n != null) {
p = n;
if (k < n.d) {
n = n.L;
} else if (k > n.d) {
n = n.R;
} else {
throw new IllegalArgumentException(
"The Binary Search Tree already has a node with this key: " + k);
}
}
// A rough example of how you can apporach insertion of the new node in the tree using BST
TreeNode newN = new TreeNode(k);
newN.clr = red;
if (p == null) {
r = newN;
} else if (k < p.d) {
p.L = newN;
} else {
pt.R = newN;
}
newN.p = p;
// Fixing the tree after the insetion
fixingTreeAfterInsertion(newN);
}
Application of Red-Black Tree
In the Java Collections Library, red-black trees have been used in the TreeSet, TreeMap, and Hashmap. It is also used in the Linux kernels: Completely Fair Scheduler, File, Memory, and Mapping.
Also, Linux uses it in the mmap and munmap operations. In addition, they are applied to reduce time complexity in the K-mean clustering algorithm.
Furthermore, MySQL implements the Red-Black tree for table searches. Why do we use it?
The Red-Black trees ensure an insertion and deletion time of O(log(n)). They are stable search trees, and as such, they always maintain a log height (n).
Think about putting the integers 1,2,3,4,5 into a binary tree. It will make 1 the root, and all succeeding elements will proceed to the right, making a linked list in effect (and each operation will require O(n) time).
Even though the average amount of time complexity will be the same, if we consider the worst case, red-black trees exceed binary search trees in terms of time complexity.
Summary
This tutorial taught you what a red-black tree is, what rules govern it, and how these rules are evaluated. We have also roughly demonstrated how you could approach it using a Java program.
Some of the important contents in this tutorial:
- Introduction to Red-Black Tree
- A typical red-black tree: Demonstration example
- Attributes of the Nodes in the Tree
- Determine the balance of the red and black tree using the data structure
- Subtree rotation of the red-black tree
- Right rotation
- Left Rotation
- Demo code examples of rotating, searching and insertion
References
Sarwan Soomro is a freelance software engineer and an expert technical writer who loves writing and coding. He has 5 years of web development and 3 years of professional writing experience, and an MSs in computer science. In addition, he has numerous professional qualifications in the cloud, database, desktop, and online technologies. And has developed multi-technology programming guides for beginners and published many tech articles.
LinkedIn