How to Determine the Height of the Binary Search Tree in Java
- the Binary Search Tree
- Application of the Binary Search Tree
- Determine the Height of Binary Search Tree
In this in-depth article, we will learn the basics of a Binary Search Tree before implementing a recursive search program to determine the height of a tree in our Java program. To understand this tutorial, we recommend you have a basic understanding of the data structure concepts of trees.
the Binary Search Tree
Let’s keep it simple. We will not bore you with the lengthy theoretical concept. However, the following are the core concepts you should be familiar with:
- A single reference to the root node of a hierarchical data structure.
- A maximum of two child nodes (a left and a right child) exist for each node.
- The Binary Search feature organizes nodes:
- Each node is sorted according to a key data field(s).
- The key of each node in the tree is greater than the key of its left child and must be less than the key of its right child.
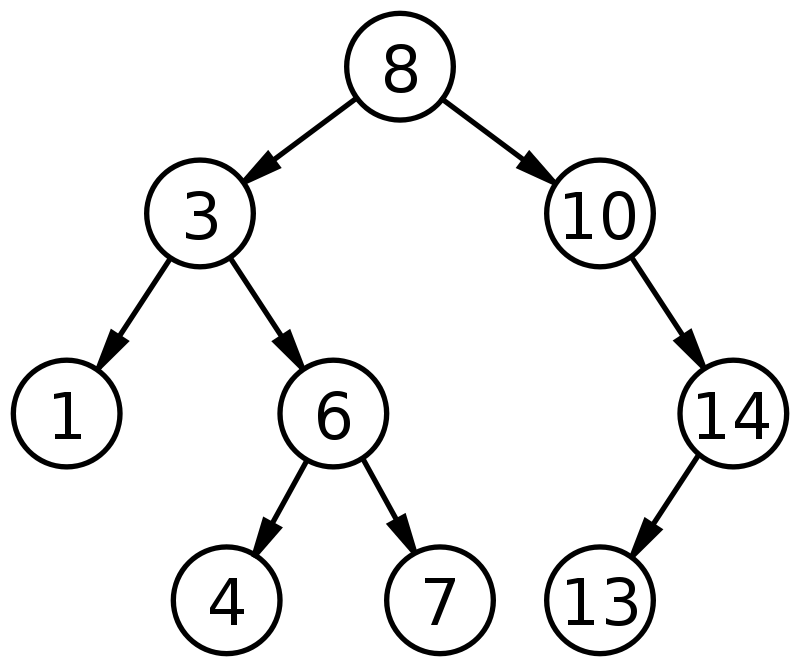
- Figure: Binary Search Tree:
Application of the Binary Search Tree
Let’s keep it simple. We will not bore you with the lengthy theoretical concept.
However, the following are the core concepts you should be familiar with:
-
You can also use a BST, where the flow and structure of data are constantly entering or leaving, such as the
mapandsetmethods in most programming languages, including Java. -
We can also use BST in three-dimensional video games to determine the position of objects and the rendering process. Read more about space partition using BST: Binary Space Partition.
-
If we mainly talk about networking, we can use these trees in almost every high bandwidth router for storing router tables; Binary Tries.
-
If you are interested in torrents and the unique generation of image signatures. Suppose you want to verify the hash needs, but the whole file is not available.
That is also where you can make use of BST. Read more: Hash Trees
In a nutshell, we can use Binary Search Trees in various applications, thanks to their ability to help arrange the data we want. We can do multi-level indexing using a Binary Search Tree.
Additionally, we can also use them for implementing different search algorithms. Since BSTs can help keep a sorted stream of data.
Determine the Height of Binary Search Tree
Determining the height of a Binary Search Tree is not a difficult task if you follow these easy steps:
-
The length of the longest path from the root to a leaf node determines the height of a binary tree. It is also known as the depth of a binary tree.
The height of the root equals the height of the tree.
-
A node’s depth is the length of the path to its root.
-
To calculate the tree’s height, we must count the number of edges between the root and the farthest leaf.
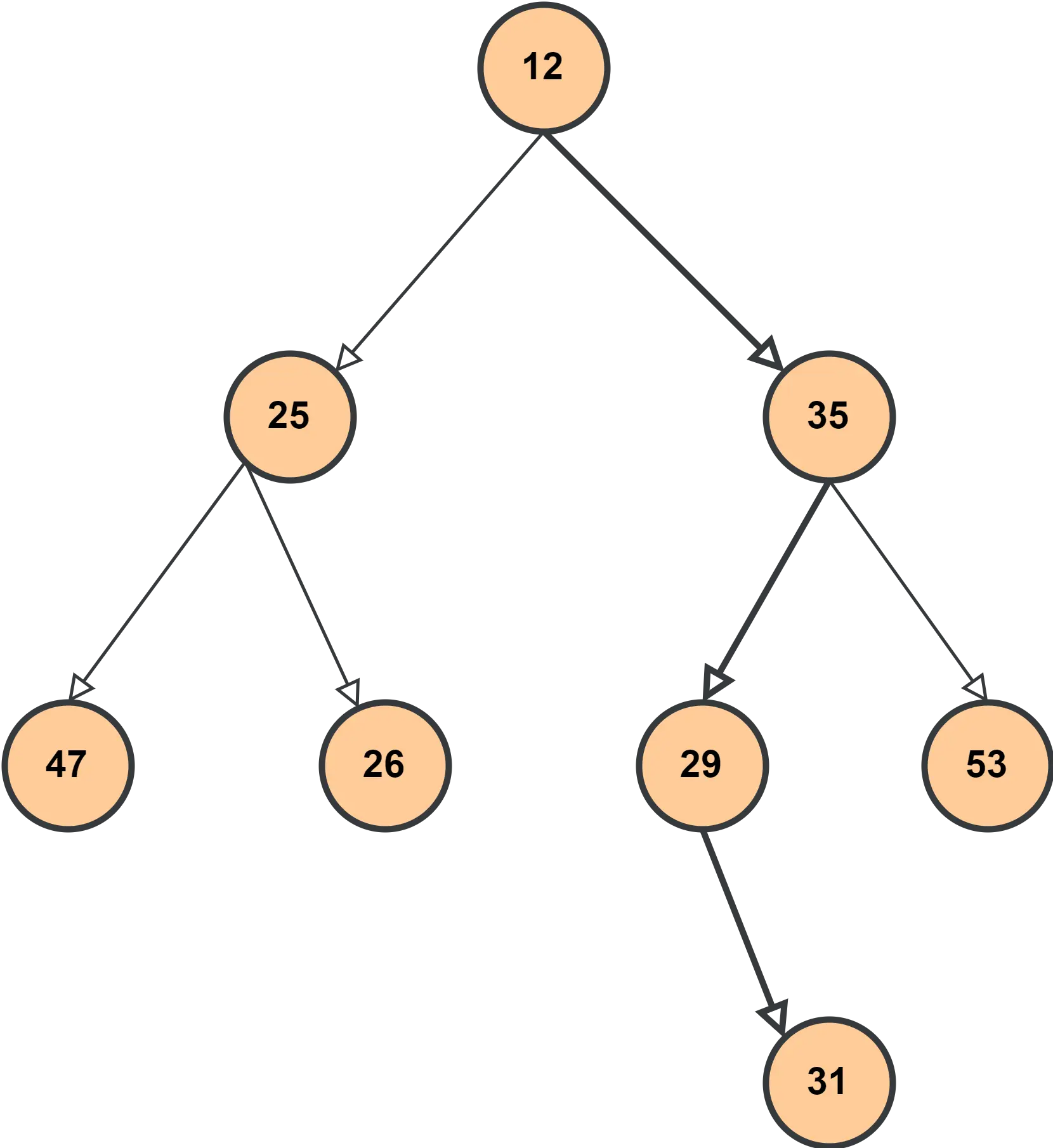
As you see in the graph above, the number of edges between the root and the farthest leaf is 3. Hence, the tree’s height is also 3.
Search for a Specific Key in the Binary Search Tree
You can search for a specific key in a Binary Search Tree recursively or iteratively. Both of these methods are popular choices for various data structure operations.
If we talk about the recursive search method, the search process begins with an examination of the root node. In this regard, suppose the tree is nil, then the key sought does not exist in the tree.
If the search result is successful, the node is returned if the key matches the root. However, suppose that the key is smaller than the root, and then the program search moves to the left subtree.
Recursive Steps to Find Height of Binary Search Tree
You should note that if the tree is empty, its height is 0. On the contrary, you need to begin from the top node down.
Suppose we want to determine the maximum depth of the left sub-tree recursively. The maximum depth of these two is the height of the binary tree (left and right subtrees).
Check out the following Pseudocode.
BinarySearchTree(a, k)
if a = NIL or k = a.key then
return a
if k < a.key then
return Tree-Search(a.L, k)
else
return Tree-Search(a.R, k)
end if
Let us implement our program recursively to search the height within a BST.
Example:
package heightofbinarysearchBSTree.delftstack;
// Java program to find the height of BSTree
// A binary BSTree BSTreeNode
public class DetHeight {
int BSTreedata;
DetHeight BSTreeNodeLeft, BSTreeNoderight;
DetHeight(int i) {
BSTreedata = i;
BSTreeNodeLeft = BSTreeNoderight = null;
}
}
class BST {
DetHeight BSTreeroot;
/* Compute the "MaximumHeight" of a BSTree -- the number of
BSTreeNodes along the longest path from the BSTreeroot BSTreeNode
down to the farthest leaf BSTreeNode.*/
int MaximumHeight(DetHeight BSTreeNode) {
if (BSTreeNode == null)
return -1;
else {
/* compute the depth of each subBSTree */
int LeftHeight = MaximumHeight(BSTreeNode.BSTreeNodeLeft);
int Rightheight = MaximumHeight(BSTreeNode.BSTreeNoderight);
/* use the larger one */
if (LeftHeight > Rightheight)
return (LeftHeight + 1);
else
return (Rightheight + 1);
}
}
/* Driver program to test above functions */
public static void main(String[] args) {
BST BSTree = new BST();
BSTree.BSTreeroot = new DetHeight(12);
BSTree.BSTreeroot.BSTreeNodeLeft = new DetHeight(25);
BSTree.BSTreeroot.BSTreeNoderight = new DetHeight(35);
BSTree.BSTreeroot.BSTreeNodeLeft.BSTreeNodeLeft = new DetHeight(47);
BSTree.BSTreeroot.BSTreeNodeLeft.BSTreeNoderight = new DetHeight(26);
BSTree.BSTreeroot.BSTreeNoderight.BSTreeNodeLeft = new DetHeight(29);
BSTree.BSTreeroot.BSTreeNoderight.BSTreeNoderight = new DetHeight(53);
BSTree.BSTreeroot.BSTreeNoderight.BSTreeNodeLeft.BSTreeNoderight = new DetHeight(31);
System.out.println("Height of BSTree is : " + BSTree.MaximumHeight(BSTree.BSTreeroot));
}
}
Output:
The height of this tree : 3
Complexity of the Search Program
In this particular case, it is linear, for we are traversing all nodes of the binary tree recursively while maintaining the height. Therefore, the time complexity is O(N), where N is the number of nodes in the tree.
Sarwan Soomro is a freelance software engineer and an expert technical writer who loves writing and coding. He has 5 years of web development and 3 years of professional writing experience, and an MSs in computer science. In addition, he has numerous professional qualifications in the cloud, database, desktop, and online technologies. And has developed multi-technology programming guides for beginners and published many tech articles.
LinkedIn